初中数学点的坐标填空题

如图，在平面直角坐标系中，点 $A$的坐标是　　．

如图，在平面直角坐标系 $\mathit{xOy}$中，点 $\mathit{A}$、 $\mathit{B}$、 $\mathit{P}$的坐标分别为 $\mathit{(}\mathit{1}\mathit{,}\mathit{0}\mathit{)}$， $\mathit{(}\mathit{2}\mathit{,}\mathit{5}\mathit{)}$， $\mathit{(}\mathit{4}\mathit{,}\mathit{2}\mathit{)}$．若点 $\mathit{C}$在第一象限内，且横坐标、纵坐标均为整数， $\mathit{P}$是 $\mathit{\Delta ABC}$的外心，则点 $\mathit{C}$的坐标为　               　．

现有四张正面分别标有数字 $-1$，1，2，3的不透明卡片，它们除数字外其余完全相同，将它们背面朝上洗均匀，随机抽取一张，记下数字后放回，背面朝上洗均匀，再随机抽取一张记下数字，前后两次抽取的数字分别记为 $m$， $n$．则点 $P(m,n)$在第二象限的概率为　　．

点 $(-1,2)$所在的象限是第　    　象限．

从1、 $-1$、0三个数中任取两个不同的数作为点的坐标，则该点在坐标轴上的概率是　　．

点 $P(m,2)$在第二象限内，则 $m$的值可以是（写出一个即可）　　．

若从 $-1$，1，2这三个数中，任取两个分别作为点 $M$的横、纵坐标，则点 $M$在第二象限的概率是　　．

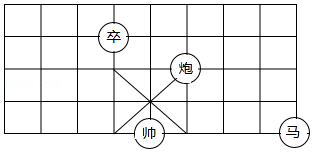
中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点 $(0,-2)$，“马”位于点 $(4,-2)$，则“卒”位于点　　．

以方程组 $\left\{\begin{array}{c}y=2x+2\\ y=-x+1\end{array}\right.$的解为坐标的点 $(x,y)$在第　   　象限．

$P(3,-4)$到 $x$轴的距离是　　．

平面直角坐标系中有两点M（a，b），N（c，d），规定（a，b）⊕（c，d）＝（a+c，b+d），则称点Q（a+c，b+d）为M，N的“和点”．若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形，则称这个四边形为“和点四边形”，现有点A（2，5），B（﹣1，3），若以O，A，B，C四点为顶点的四边形是“和点四边形”，则点C的坐标是　      ．

点 $P（x﹣2，x+3）$在第一象限，则x的取值范围是   ．

如图，方格纸上每个小正方形的边长均为1个单位长度，点 $O$， $A$， $B$， $C$在格点（两条网格线的交点叫格点）上，以点 $O$为原点建立直角坐标系，则过 $A$， $B$， $C$三点的圆的圆心坐标为　　．

从 $-1$，0，1，2这四个数中，任取两个不同的数作为点的坐标，则该点在第一象限的概率为　　．

在平面直角坐标系中，对于平面内任一点 $(a,b)$，若规定以下三种变换：

①△ $(a$， $b)=(-a$， $b)$；

②〇 $(a$， $b)=(-a$， $-b)$；

③ $\Omega (a$， $b)=(a$， $-b)$，

按照以上变换例如：△ $($〇 $(1$， $2\left)\right)=(1$， $-2)$，则〇 $\left(\Omega \right(3,4\left)\right)$等于　　．