阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
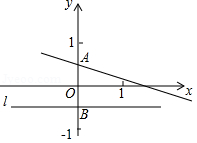
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
如图,在直角坐标系 中,菱形 的边 在 轴正半轴上,点 , 在第一象限, ,边长 .点 从原点 出发沿 轴正半轴以每秒1个单位长的速度作匀速运动,点 从 出发沿边 以每秒2个单位长的速度作匀速运动,过点 作直线 垂直于 轴并交折线 于 ,交对角线 于 ,点 和点 同时出发,分别沿各自路线运动,点 运动到原点 时, 和 两点同时停止运动.
(1)当 时,求线段 的长;
(2)求 为何值时,点 与 重合;
(3)设 的面积为 ,求 与 的函数关系式及 的取值范围.

已知:如图所示,在平面直角坐标系 中, , , ,若点 是边 上的一个动点(与点 、 不重合),过点 作 交 于点 .
(1)求点 的坐标;
(2)当 的周长与四边形 的周长相等时,求 的长;
(3)在 上是否存在点 ,使得 为等腰直角三角形?若存在,请求出此时 的长;若不存在,请说明理由.
