小明为画一个零件的轴截面,以该轴截面底边所在的直线为 轴,对称轴为 轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取 ,则图中转折点 的坐标表示正确的是

A. B. C. D.
我们把1,1,2,3,5,8,13,21, 这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作 圆弧 , , , 得到斐波那契螺旋线,然后顺次连接 , , , 得到螺旋折线(如图),已知点 , , ,则该折线上的点 的坐标为
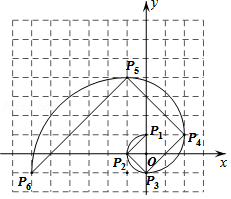
A. B. C. D.
如图,在直角坐标系中,点 在函数 的图象上, 轴于点 , 的垂直平分线与 轴交于点 ,与函数 的图象交于点 ,连接 , , , ,则四边形 的面积等于

A.2B. C.4D.
如图,一直线与两坐标轴的正半轴分别交于 , 两点, 是线段 上任意一点(不包括端点),过 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是
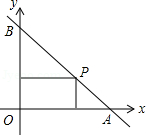
A. B. C. D.
在平面直角坐标系内,以原点 为圆心,1为半径作圆,点 在直线 上运动,过点 作该圆的一条切线,切点为 ,则 的最小值为
A.3B.2C. D.
如图,过点 作直线
作直线 的垂线,垂足为点
的垂线,垂足为点 ,过点
,过点 作
作 轴,垂足为点
轴,垂足为点 ,过点
,过点 作
作 ,垂足为点
,垂足为点 ,
, ,这样依次下去,得到一组线段:
,这样依次下去,得到一组线段: ,
, ,
, ,
, ,则线段
,则线段 的长为
的长为


A. B.
B. C.
C. D.
D.
如图,在矩形 中,
中, 为坐标原点,
为坐标原点, 、
、 分别在
分别在 轴、
轴、 轴上,点
轴上,点 的坐标为
的坐标为 ,
, ,
, ,将
,将 沿
沿 所在直线对折后,点
所在直线对折后,点 落在点
落在点 处,则点
处,则点 的坐标为
的坐标为


A. ,
, B.
B. C.
C. ,
, D.
D. ,
,
在平面直角坐标系中,点 是线段 上一点,以原点 为位似中心把 放大到原来的两倍,则点 的对应点的坐标为
A. B. 或
C. , D. , 或 ,
如图,平面直角坐标系中, 经过三点 , , ,点 是 上的一动点.当点 到弦 的距离最大时, 的值是

A.2B.3C.4D.5
如图,平面直角坐标系 中,矩形 的边 、 分别落在 、 轴上,点 坐标为 ,反比例函数 的图象与 边交于点 ,与 边交于点 ,连接 ,将 沿 翻折至△ 处,点 恰好落在正比例函数 图象上,则 的值是

A. B. C. D.
已知 、 、 为常数,点 在第二象限,则关于 的方程 根的情况是
A.有两个相等的实数根B.有两个不相等的实数根
C.没有实数根D.无法判断