初中数学平面直角坐标系选择题

在平面直角坐标系中，点 $P(m+1,2-m)$在第二象限，则 $m$的取值范围为 $($　　 $)$

A． $m<-1$B． $m<2$C． $m>2$D． $-1<m<2$

如图，在单位长度为1米的平面直角坐标系中，曲线是由半径为2米，圆心角为 $120°$ 的 $\stackrel{̂}{\mathit{AB}}$ 多次复制并首尾连接而成．现有一点 $P$ 从 $A(A$ 为坐标原点）出发，以每秒 $\frac{2}{3}\pi$ 米的速度沿曲线向右运动，则在第2019秒时点 $P$ 的纵坐标为 $($ 　　 $)$

A．

$-2$

B．

$-1$

C．

0

D．

1

若点 $A(a+1,b-2)$在第二象限，则点 $B(-a,1-b)$在 $($　　 $)$

A．第一象限B．第二象限C．第三象限D．第四象限

如图， $\odot P$ 与 $x$ 轴交于点 $A(-5,0)$ ， $B(1,0)$ ，与 $y$ 轴的正半轴交于点 $C$ ．若 $\angle \mathit{ACB}=60°$ ，则点 $C$ 的纵坐标为 $($ 　　 $)$

A．

$\sqrt{13}+\sqrt{3}$

B．

$2\sqrt{2}+\sqrt{3}$

C．

$4\sqrt{2}$

D．

$2\sqrt{2}+2$

如图，已知矩形 $\mathit{ABCD}$的顶点 $A$， $D$分别落在 $x$轴、 $y$轴上， $\mathit{OD}=2\mathit{OA}=6$， $\mathit{AD}:\mathit{AB}=3:1$，则点 $C$的坐标是 $($　　 $)$

A． $(2,7)$B． $(3,7)$C． $(3,8)$D． $(4,8)$

在平面直角坐标系中，一个智能机器人接到的指令是：从原点 $O$ 出发，按"向上 $\to$ 向右 $\to$ 向下 $\to$ 向右"的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点 $A_1$ ，第二次移动到点 $A_2\dots \dots$ 第 $n$ 次移动到点 $A_n$ ，则点 $A_{2019}$ 的坐标是 $($ 　　 $)$

A．

$(1010,0)$

B．

$(1010,1)$

C．

$(1009,0)$

D．

$(1009,1)$

已知直线 $y=-x+1$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ 、 $B$ 两点，点 $P$ 是第一象限内的点，若 $\mathit{\Delta PAB}$ 为等腰直角三角形，则点 $P$ 的坐标为 $($ 　　 $)$

A．	$(1,1)$
B．	$(1,1)$ 或 $(1,2)$
C．	$(1,1)$ 或 $(1,2)$ 或 $(2,1)$
D．	$(0,0)$ 或 $(1,1)$ 或 $(1,2)$ 或 $(2,1)$

如图，在平面直角坐标系中，直线 $l_1:y=\frac{\sqrt{3}}{3}x+1$ 与直线 $l_2:y=\sqrt{3}x$ 交于点 $A_1$ ，过 $A_1$ 作 $x$ 轴的垂线，垂足为 $B_1$ ，过 $B_1$ 作 $l_2$ 的平行线交 $l_1$ 于 $A_2$ ，过 $A_2$ 作 $x$ 轴的垂线，垂足为 $B_2$ ，过 $B_2$ 作 $l_2$ 的平行线交 $l_1$ 于 $A_3$ ，过 $A_3$ 作 $x$ 轴的垂线，垂足为 $B_3\dots$ 按此规律，则点 $A_n$ 的纵坐标为 $($ 　　 $)$

A．

${\left(\frac{3}{2}\right)}^n$

B．

${\left(\frac{1}{2}\right)}^n+1$

C．

${\left(\frac{3}{2}\right)}^{n-1}+\frac{1}{2}$

D．

$\frac{3^n-1}{2}$

矩形 $\mathit{OABC}$在平面直角坐标系中的位置如图所示，点 $B$的坐标为 $(3,4)$， $D$是 $\mathit{OA}$的中点，点 $E$在 $\mathit{AB}$上，当 $\mathit{\Delta CDE}$的周长最小时，点 $E$的坐标为 $($　　 $)$

A． $(3,1)$B． $(3,\frac{4}{3})$C． $(3,\frac{5}{3})$D． $(3,2)$

如图所示，小球从台球桌面 $\mathit{ABCO}$ 上的点 $P(0,1)$ 出发，撞击桌边发生反弹，反射角等于入射角若小球以每秒 $\sqrt{2}$ 个单位长度的速度沿图中箭头方向运动，则第50秒的小球所在位置的坐标为 $($ 　　 $)$

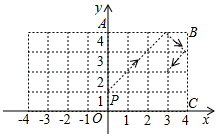
A．

$(2,3)$

B．

$(3,4)$

C．

$(3,2)$

D．

$(0,1)$

我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形 $\mathit{ABCD}$ 的边 $\mathit{AB}$ 在 $x$ 轴上， $\mathit{AB}$ 的中点是坐标原点 $O$ ，固定点 $A$ ， $B$ ，把正方形沿箭头方向推，使点 $D$ 落在 $y$ 轴正半轴上点 $D\text{'}$ 处，则点 $C$ 的对应点 $C\text{'}$ 的坐标为 $($ 　　 $)$

A．

$(\sqrt{3}$ ， $1)$

B．

$(2,1)$

C．

$(1,\sqrt{3})$

D．

$(2,\sqrt{3})$

如图，在平面直角坐标系中，以 O为圆心，适当长为半径画弧，交 x轴于点 M，交 y轴于点 N，再分别以点 M， N为圆心，大于 MN的长为半径画弧，两弧在第二象限交于点 P，若点 P的坐标为（3 a， b+1），则 a与 b的数量关系为（　　）

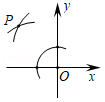
A．

3a＝2b

B．

3a＝b+1

C．

3a+b﹣1＝0

D．

3a＝﹣b﹣1

在平面直角坐标系的第二象限内有一点 $M$，点 $M$到 $x$轴的距离为3，到 $y$轴的距离为4，则点 $M$的坐标是 $($　　 $)$

A． $(3,-4)$B． $(4,-3)$C． $(-4,3)$D． $(-3,4)$

对于任意实数 $m$，点 $P(m-2,9-3m)$不可能在 $($　　 $)$

A．第一象限B．第二象限C．第三象限D．第四象限

下列运算及判断正确的是（　　）

A．	﹣5× $\frac{1}{5}$ ÷（﹣ $\frac{1}{5}$ ）×5＝1
B．	方程（x ^2+x﹣1） ^x ^+3＝1有四个整数解
C．	若a×567 ^3＝10 ^3，a÷10 ^3＝b，则a×b＝ $\frac{{10}^3}{{567}^6}$
D．	有序数对（m ^2+1，|m|）在平面直角坐标系中对应的点一定在第一象限