关于 的一元二次方程 的两实数根 , ,满足 ,则 的值是
| A. |
8 |
B. |
32 |
C. |
8或32 |
D. |
16或40 |
函数 的图象如图所示,则关于 的一元二次方程 的根的情况是
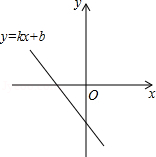
| A. |
没有实数根 |
B. |
有两个相等的实数根 |
| C. |
有两个不相等的实数根 |
D. |
无法确定 |
关于 x的一元二次方程 有实数根,则 a的取值范围是( )
| A. |
且 |
B. |
|
C. |
且 |
D. |
|
已知关于 的一元二次方程 ,其中 , 在数轴上的对应点如图所示,则这个方程的根的情况是
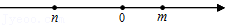
| A. |
有两个不相等的实数根 |
B. |
有两个相等的实数根 |
| C. |
没有实数根 |
D. |
无法确定 |
已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是
| A. |
|
B. |
|
C. |
且 |
D. |
且 |
关于 的一元二次方程 的根的情况,下列说法正确的是
| A. |
有两个不相等的实数根 |
B. |
有两个相等的实数根 |
| C. |
无实数根 |
D. |
无法确定 |
关于 的一元二次方程 有两个不相等的实数根,则 的值可能是
| A. |
8 |
B. |
9 |
C. |
10 |
D. |
11 |
对于实数 , 定义运算"☆"如下: ☆ ,例如3☆ ,则方程1☆ 的根的情况为
| A. |
没有实数根 |
B. |
只有一个实数根 |
| C. |
有两个相等的实数根 |
D. |
有两个不相等的实数根 |
在平面直角坐标系中,若直线 不经过第一象限,则关于 的方程 的实数根的个数为
| A. |
0个 |
B. |
1个 |
C. |
2个 |
D. |
1或2个 |
对于一元二次方程 ,则它根的情况为
| A. |
没有实数根 |
B. |
两根之和是3 |
| C. |
两根之积是 |
D. |
有两个不相等的实数根 |
关于 的一元二次方程 根的情况,下列说法正确的是
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.无法确定