(1)在下列横线上用含有a,b的代数式表示相应图形的面积.
① ② ③ ④
(2)通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示 ;
(3)利用(2)的结论计算9972+6×997+9的值.

如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方
形,然后按图②的方式拼成一个正方形。
(1)你认为图②中的阴影部分的正方形的边长等于_______________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积。
方法①______________.
方法②______________.
(3)观察图②,你能写出 ,
, ,mn这三个代数式间的等量关系吗?
,mn这三个代数式间的等量关系吗?
图1是一个长为2 ,宽为2
,宽为2 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.

(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形.利用阴影部分面积的不同表示方法,直接写出代数式( )2、(
)2、( )2、
)2、 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含 、
、 的代数式表示).
的代数式表示).
图①是一个长为 、宽为
、宽为 的长方形,用这样四个全等的长方形,拼成如图②的正方形.
的长方形,用这样四个全等的长方形,拼成如图②的正方形.

(1)按要求填空:
ⅰ.请用含字母 、
、 的代数式表示图②中的阴影部分的正方形的边长: ;
的代数式表示图②中的阴影部分的正方形的边长: ;
ⅱ.请用含字母 、
、 的代数式,用两种不同的方法表示图②中阴影部分的面积:
的代数式,用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
ⅲ.观察图②,请写出代数式 、
、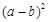 、
、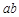 之间的等量关系: ;
之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:
若 ,
, ,求
,求 的值.
的值.