如图,将一枚跳棋放在七边形 的顶点 处,按顺时针方向移动这枚跳棋2020次.移动规则是:第 次移动 个顶点(如第一次移动1个顶点,跳棋停留在 处,第二次移动2个顶点,跳棋停留在 处),按这样的规则,在这2020次移动中,跳棋不可能停留的顶点是

| A. |
、 |
B. |
、 |
C. |
、 、 |
D. |
、 、 |
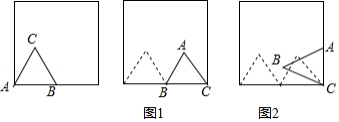
如图,边长为1的正三角形 放置在边长为2的正方形内部,顶点 在正方形的一个顶点上,边 在正方形的一边上,将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第1次无滑动滚动(如图 ;再将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第2次无滑动滚动(如图 , ,每次旋转的角度都不大于 ,依次这样操作下去,当完成第2016次无滑动滚动时,点 经过的路径总长为 .
如图各图形是由大小相同的黑点组成,图1中有2个点,图2中有7个点,图3中有14个点,,按此规律,第10个图中黑点的个数是 .

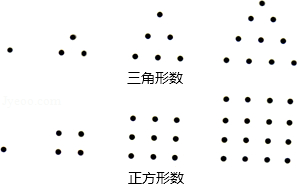
我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为 ,最大的“正方形数”为 ,则 的值为
A.33B.301C.386D.571
如图,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第20个图需要黑色棋子的个数为 .

如图,在平面直角坐标系中,将边长为1的正方形 绕点 顺时针旋转 后得到正方形 ,依此方式,绕点 连续旋转2019次得到正方形 ,那么点 的坐标是

| A. |
, |
B. |
|
C. |
, |
D. |
|
如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形 按此规律摆下去,第 个图案有 个三角形(用含 的代数式表示).

如图, 的面积为 .点 , , , , 是边 的 等分点 ,且 为整数),点 , 分别在边 , 上,且 ,连接 , , , , ,连接 , , , , ,线段 与 相交于点 ,线段 与 相交于点 ,线段 与 相交于点 , ,线段 与 相交于点 ,则△ ,△ ,△ , ,△ 的面积和是 .(用含有 与 的式子表示)

下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第
个图形共有210个小球.

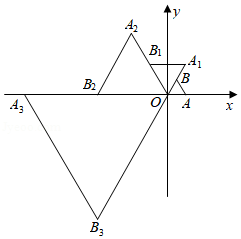
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
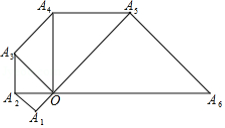
如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
A. B. C. D.
如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第 个图案中白色正方形比黑色正方形多 个.(用含 的代数式表示)

在公园内,牡丹按正方形种植,在它的周围种植芍药,如图反映了牡丹的列数 和芍药的数量规律,那么当 时,芍药的数量为
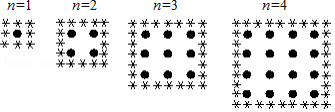
A.84株B.88株C.92株D.121株