用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )

| A.x(10-x)平方米 |
| B.x(10-3x)平方米 |
C. 平方米 平方米 |
D. 平方米 平方米 |
用10米长的铝合金做成一个长方形的窗框(如图),设长方形窗框的横条长度为x米,则长方形窗框的面积为( )

| A.x(10﹣x)平方米 |
| B.x(10﹣3x)平方米 |
C. 平方米 平方米 |
D. 平方米 平方米 |
点 , , , 在数轴上的位置如图所示, 为原点, , .若点 所表示的数为 ,则点 所表示的数为

| A. |
|
B. |
|
C. |
|
D. |
|
某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带 条(
条( >20).
>20).
(1)若该客户按方案①购买,需付款________元(用含 的代数式表示);若该客户按方案②购买,需付款________元(用含
的代数式表示);若该客户按方案②购买,需付款________元(用含 的代数式表示).
的代数式表示).
(2)若 =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
某校七年级四个班的学生在植树节这天共义务植树(6a-3b)棵,一班植树a棵,二班植树的棵数比一班的两倍少b棵,三班植树的棵数比二班的一半多1棵.
(1)求三班的植树棵数(用含a,b的式子表示);
(2)求四班的植树棵数(用含a,b的式子表示);
(3)若四个班共植树54棵,求二班比三班多植树多少棵?
一座楼梯的示意图如图所示,要在楼梯上铺一条地毯.
(1)地毯至少需多少长?(用关于a,h的代数式表示)
(2)若楼梯的宽为b,则地毯的面积为多少?
(3)当a=5m,b=1.2m,h=3m时,则地毯的面积是多少m2
对于任意一个四位数 ,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数 为"共生数".例如: ,因为 ,所以3507是"共生数"; ,因为 ,所以4135不是"共生数".
(1)判断5313,6437是否为"共生数"?并说明理由;
(2)对于"共生数" ,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记 .求满足 各数位上的数字之和是偶数的所有 .
“绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向 , 两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥; , 两个果园分别需用110吨和70吨有机化肥.两个仓库到 , 两个果园的路程如表所示:
路程(千米) |
||
甲仓库 |
乙仓库 |
|
果园 |
15 |
25 |
果园 |
20 |
20 |
设甲仓库运往 果园 吨有机化肥,若汽车每吨每千米的运费为2元,
(1)根据题意,填写下表.
运量(吨 |
运费(元 |
|||
甲仓库 |
乙仓库 |
甲仓库 |
乙仓库 |
|
果园 |
|
|
|
|
果园 |
|
|
|
|
(2)设总运费为 元,求 关于 的函数表达式,并求当甲仓库运往 果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?
某市出租车收费标准是:起步价10元,可乘3千米;3千米到5千米,每千米1.3元;超过5千米,每千米2.4元。
(1)若某人乘坐了 (
(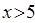 )千米的路程,则他应支付的费用是多少?
)千米的路程,则他应支付的费用是多少?
(2)若某人乘坐的路程为6千米,那么他应支付的费用是多少?