如图,在平面直角坐标系xOy中,矩形AOCD的顶点A的坐标是(0,4),现有两动点P,Q,点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.点P,Q同时出发,同时停止,设运动时间为t(秒),当t=2(秒)时,PQ=2 .
.
(1)求点D的坐标,并直接写出t的取值范围;
(2)连接AQ并延长交x轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF,则△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值;
(3)在(2)的条件下,t为何值时,四边形APQF是梯形?
如图,△ABC中,∠C = 90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ .在整个运动过程中,△MPQ的面积大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减小
如图(甲),扇形OAB的半径OA=6,圆心角∠AOB=90°,C是 上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点H在线段DE上,且EH=
上不同于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点H在线段DE上,且EH= DE.设EC的长为x,△CEH的面积为y,图(乙)中表示y与x的函数关系式的图象可能是( )
DE.设EC的长为x,△CEH的面积为y,图(乙)中表示y与x的函数关系式的图象可能是( )

某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的余油量y(L)与工作时间x(h)之间为一次函数关系,如图所示.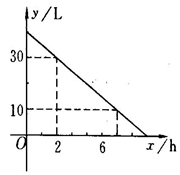
(1)求y与x的函数解析式.
(2)一箱油可供拖位机工作几小时?
利用计算器求值时,小明将按键顺序为 显示结果记为
,
显示结果记为
,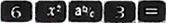 的显示结果记为
.则
,
的大小关系为
的显示结果记为
.则
,
的大小关系为
A. B. C. D.不能比较
函数y=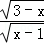 中x的取值范围是( )
中x的取值范围是( )
| A.x≤3 | B.x≠1 | C.x≤3且x≠1 | D.1<x≤3 |
如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数, ≈1.7,
≈1.7, ≈1.4 )
≈1.4 )
2015年4月l8日周杰伦“摩天轮2”演唱会在重庆奥体中心如期举行.小王开车从家出发前去观看,预计1个小时能到达,可当天路上较为拥堵,行驶了半个小时,刚好行驶了一半路程,道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是小王将车停在轻轨站的车库,然后坐轻轨前往,结果按预计时间到达.下面能反映小王距离奥体中心的距离y (千米)与时间x (小时)的函数关系的大致图象是
( )