(满分9分)如图,公园入口处原有三级台阶,每级台阶高为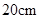 ,深为
,深为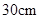 ,为方便残疾人士,拟将台阶改成斜坡,台阶的起点为
,为方便残疾人士,拟将台阶改成斜坡,台阶的起点为 ,斜坡的起始点为
,斜坡的起始点为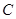 (如图所示),如果斜坡的坡角
(如图所示),如果斜坡的坡角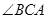 设计为
设计为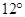 ,那么斜坡起点
,那么斜坡起点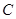 应离
应离 点多远?
点多远?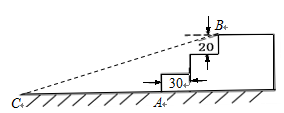
(精确到 ,参考数据:
,参考数据: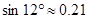 ,
,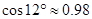 ,
, )
)
(本题8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据: ,
,
“东方之星”客船失事之后,本着“关爱生命,救人第一”的宗旨.搜救部门紧急派遣直升机到失事地点进行搜救,搜救过程中,假设直升机飞到A处时,发现前方江面上B处有一漂浮物,从A测得B处的俯角为30°,已知该直升机一直保持在距江面100米高度飞行搜索,飞行速度为10米每秒,求该直升机沿直线方向朝漂浮物飞行多少秒可到达漂浮物的正上方?(结果精确到0.1, ≈1.73)
≈1.73)
若点P(a,b)在第四象限,则Q(-a,b-1)在( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
函数 中自变量
中自变量 的取值范围是( ).
的取值范围是( ).
| A.x≥-3 | B. |
C.x≥-3或 |
D.x≥-3且 |
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为
| A.20米 | B.10 米 米 |
C.15 米 米 |
D.5 米 米 |
已知一个函数,当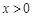 时,函数值
时,函数值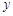 随着
随着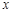 的增大而减小,请写出这个函数关系式 (写出一个即可).
的增大而减小,请写出这个函数关系式 (写出一个即可).