初中数学有理数的混合运算试题

出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的，如果规定向东为正，向西为负，他这天下午行车里程（单位：千米）如下：+15，－2．5，+5，－1，+10．5，－3，－2，+12，+4，－5，+6．
（1）若小李出发地记为0，他将最后一名乘客送抵目的地小李距出发地点有多远？
（2）若汽车耗油量为0．4升/ 千米，这天下午小李共耗油多少升？

计算：．

如果a、b互为倒数，c、d互为相反数，且m=-1，则代数式2ab-（c+d）+m²=_______．

阅读理解： $a$， $b$， $c$， $d$是实数，我们把符号 $\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|$称为 $2\times 2$阶行列式，并且规定： $\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=a\times d-b\times c$，例如： $\left|\begin{array}{cc}3& 2\\ -1& -2\end{array}\right|=3\times (-2)-2\times (-1)=-6+2=-4$．二元一次方程组 $\left\{\begin{array}{c}{a}_{1}x+b_{1}y=c_1\\ a_{2}x+b_{2}y=c_2\end{array}\right.$的解可以利用 $2\times 2$阶行列式表示为： $\left\{\begin{array}{c}x=\frac{D_x}{D}\\ y=\frac{D_y}{D}\end{array}\right.$；其中 $D=\left|\begin{array}{cc}{a}_1& b_1\\ a_2& b_2\end{array}\right|$， $D_x=\left|\begin{array}{cc}{c}_1& b_1\\ c_2& b_2\end{array}\right|$， $D_y=\left|\begin{array}{cc}{a}_1& c_1\\ a_2& c_2\end{array}\right|$．

问题：对于用上面的方法解二元一次方程组 $\left\{\begin{array}{c}2x+y=1\\ 3x-2y=12\end{array}\right.$时，下面说法错误的是 $($　　 $)$

A． $D=\left|\begin{array}{cc}2& 1\\ 3& -2\end{array}\right|=-7$B． $D_x=-14$

C． $D_y=27$D．方程组的解为 $\left\{\begin{array}{c}x=2\\ y=-3\end{array}\right.$

我们知道，任意一个正整数 $n$ 都可以进行这样的分解： $n=p\times q(p$ ， $q$ 是正整数，且 $p⩽q)$ ，在 $n$ 的所有这种分解中，如果 $p$ ， $q$ 两因数之差的绝对值最小，我们就称 $p\times q$ 是 $n$ 的最佳分解．并规定： $F\left(n\right)=\frac{p}{q}$ ．例如12可以分解成 $1\times 12$ ， $2\times 6$ 或 $3\times 4$ ，因为 $12-1>6-2>4-3$ ，所以 $3\times 4$ 是12的最佳分解，所以 $F\left(12\right)=\frac{3}{4}$ ．

（1）如果一个正整数 $a$ 是另外一个正整数 $b$ 的平方，我们称正整数 $a$ 是完全平方数．求证：对任意一个完全平方数 $m$ ，总有 $F\left(m\right)=1$ ；

（2）如果一个两位正整数 $t$ ， $t=10x+y(1⩽x⩽y⩽9$ ， $x$ ， $y$ 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数 $t$ 为"吉祥数"，求所有"吉祥数"中 $F\left(t\right)$ 的最大值．

按如图所示的运算程序，能使输出的结果为12的是 $($ 　　 $)$

A．

$x=3$ ， $y=3$

B．

$x=-4$ ， $y=-2$

C．

$x=2$ ， $y=4$

D．

$x=4$ ， $y=2$

计算 $6÷(-\frac{1}{2}+\frac{1}{3})$，方方同学的计算过程如下，原式 $=6÷(-\frac{1}{2})+6÷\frac{1}{3}=-12+18=6$．请你判断方方的计算过程是否正确，若不正确，请你写出正确的计算过程．

根据下列各式的规律，在横线处填空：

$\frac{1}{1}+\frac{1}{2}-1=\frac{1}{2}$， $\frac{1}{3}+\frac{1}{4}-\frac{1}{2}=\frac{1}{12}$， $\frac{1}{5}+\frac{1}{6}-\frac{1}{3}=\frac{1}{30}$， $\frac{1}{7}+\frac{1}{8}-\frac{1}{4}=\frac{1}{56}\dots$， $\frac{1}{2017}+\frac{1}{2018}-$　　 $=\frac{1}{2017\times 2018}$

我们知道，任意一个正整数 $n$ 都可以进行这样的分解： $n=p\times q(p$ ， $q$ 是正整数，且 $p⩽q)$ ，在 $n$ 的所有这种分解中，如果 $p$ ， $q$ 两因数之差的绝对值最小，我们就称 $p\times q$ 是 $n$ 的最佳分解．并规定： $F\left(n\right)=\frac{p}{q}$ ．例如12可以分解成 $1\times 12$ ， $2\times 6$ 或 $3\times 4$ ，因为 $12-1>6-2>4-3$ ，所以 $3\times 4$ 是12的最佳分解，所以 $F\left(12\right)=\frac{3}{4}$ ．

（1）如果一个正整数 $a$ 是另外一个正整数 $b$ 的平方，我们称正整数 $a$ 是完全平方数．求证：对任意一个完全平方数 $m$ ，总有 $F\left(m\right)=1$ ；

（2）如果一个两位正整数 $t$ ， $t=10x+y(1⩽x⩽y⩽9$ ， $x$ ， $y$ 为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们称这个数 $t$ 为"吉祥数"，求所有"吉祥数"中 $F\left(t\right)$ 的最大值．

计算：

（1） ${(a+b)}^2-b(2a+b)$

（2） $(\frac{2-2x}{x+1}+x-1)÷\frac{x^2-x}{x+1}$ ．

观察下列等式：

第一个等式：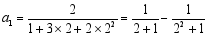

第二个等式：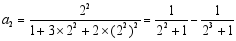

第三个等式：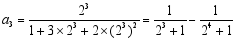

第四个等式：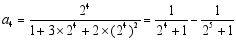

按上述规律，回答下列问题：

（1）请写出第六个等式：　　　　；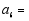

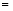（2）用含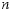的代数式表示第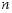个等式：　　　　；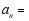

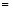（3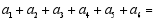）　　（得出最简结果）；

（4）计算：．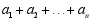

计算： $-5\times 2+3÷\frac{1}{3}-(-1)$．

下列运算错误的是 $($ 　　 $)$

A．	${(\sqrt{3}-1)}^0=1$	B．	${(-3)}^2÷\frac{9}{4}=\frac{1}{4}$
C．	$5x^2-6x^2=-x^2$	D．	${\left(2m^3\right)}^2÷{\left(2m\right)}^2=m^4$

某市前年的年均浓度为50微克立方米，去年比前年下降了，如果今年的年均浓度比去年也下降，那么今年的年均浓度将是　　微克立方米．

求两个正整数的最大公约数是常见的数学问题，中国古代数学专著《九章算术》中便记载了求两个正整数最大公约数的一种方法 $--$更相减损术，术曰：“可半者半之，不可半者，副置分母、子之数，以少成多，更相减损，求其等也．以等数约之”，意思是说，要求两个正整数的最大公约数，先用较大的数减去较小的数，得到差，然后用减数与差中的较大数减去较小数，以此类推，当减数与差相等时，此时的差（或减数）即为这两个正整数的最大公约数．

例如：求91与56的最大公约数

解：

请用以上方法解决下列问题：

（1）求108与45的最大公约数；

（2）求三个数78、104、143的最大公约数．