初中数学试题

有若干张面积分别为的正方形和长方形纸片，阳阳从中抽取了1张面积为的正方形纸片，4张面积为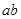的长方形纸片，若他想拼成一个大正方形，则还需要抽取面积为的正方形纸片

A．2张

B．4张

C．6张

D．8张

如图2，在平面直角坐标系中，点的坐标为（1，4）、（5，4）、（1、），则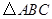外接圆的圆心坐标是

A．（2，3）

B．（3，2）

C．（1，3）

D．（3，1）

已知整式的值为6，则的值为

A．9

B．12

C．18

D．24

阳光公司销售一种进价为21元的电子产品，按标价的九折销售，仍可获得20%，则这种电子产品的标价为

A．26元

B．27元

C．28元

D．29元

“十二五”期间，新疆将建成横贯东西、沟通天山的“十”字形高速公路主骨架，全疆高速公路总里程突破4 000km，交通运输条件得到全面改善，将4 000用科学记数法可以表示为

A．

B．

C．

D．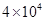

如图1是由五个相同的小正方体组成的几何体，则它的左视图是

在0，，1，这四个数中负整数是

A．

B．0

C．

D．1

下图所示的几何体中，主视图与左视图不相同的几何体是：

不等式组的正整数解有：

A．1个

B．2个

C．3个

D．4个

(10分)如图①，将两块全等的三角板拼在一起，其中△ABC的边BC在直线l上，AC⊥BC且AC = BC；△EFP的边FP也在直线l上，边EF与边AC重合，EF⊥FP且EF = FP。
（1）在图①中，请你通过观察、测量，猜想并写出AB与AP所满足的数量关系和位置关系；
（2）将三角板△EFP沿直线l向左平移到图②的位置时，EP交AC于点Q，连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；
（3）将三角板△EFP沿直线l向左平移到图③的位置时，EP的延长线交AC的延长线于点Q，连接AP、BQ。你认为（2）中猜想的BQ与AP所满足的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由。

阅读材料，解答下列问题．
例：当时，如则，故此时的绝对值是它本身
当时，，故此时的绝对值是零
当时，如则，故此时的绝对值是它的相反数
综合起来一个数的绝对值要分三种情况，即

问：(1)这种分析方法涌透了数学思想．
（2）请仿照例中的分类讨论的方法，分析二次根式的各种展开的情况．
（3）猜想与的大小关系．
（4）尝试用从以上探究中得到的结论来解决下面的问题：

（1）计算
（2）解方程：
（3）计算：

电子跳蚤游戏盘是如图所示的△ABC，AB=AC=BC=6．如果跳蚤开始时在BC边的P₀处，BP₀=2．跳蚤第一步从P₀跳到AC边的P₁（第1次落点）处，且CP₁= CP₀；第二步从P₁跳到AB边的P₂（第2次落点）处，且AP₂= AP₁；第三步从P₂跳到BC边的P₃（第3次落点）处，且BP₃= BP₂；…；跳蚤按照上述规则一直跳下去，第n次落点为P_n（n为正整数），则点P₂₀₀₉与点P₂₀₁₀之间的距离为_________．

已知，则m + n的值是________。

如图OB、AB分别表示甲、乙两名同学运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：①甲让乙先跑12米；② 甲的速度比乙快1.5米/秒；③ 8秒钟内，乙在甲前面；④ 8 秒钟后，甲超过了乙，其中正确的说法是（）


A、① ② B、① ③ ④ C、② ③ D、① ② ③ ④