高中物理试题

某同学用刻度尺测金属丝的长度L，用螺旋测微器测金属丝的直径d，其示数分别如图1和图2所示，则金属丝长度L=      cm，金属丝直径d=     mm．他还用多用电表按正确的操作程序测出了它的阻值，测量时选用“×1”欧姆挡，示数如图3所示，则金属丝的电阻R=  Ω．

如图所示，在线圈上端放置一盛有冷水的金属杯，现接通交流电源，过了几分钟，杯内的水沸腾起来．若要缩短上述加热时间，下列措施可行的有（   ）

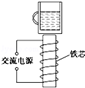
A．增加线圈的匝数

B．将金属杯换为瓷杯

C．取走线圈中的铁芯

D．提高交流电源的频率

如图所示，绝缘水平地面固定一不带电金属小球B，空间存在水平向右的匀强电场，现将一带正电荷，质量为m，与B球完全相同的小球A，从距B球S₀处由静止释放，已知A球与地面之间摩擦因数为（，其中q、E分别为A球带电量和场强大小，数值均未知），不计碰撞过程中能量的损失，小球的大小及小球间的静电力忽略不计，重力加速度为g。

求：（1）A、B两球碰前瞬间A球的速度
（2）A球最终所处的位置
（3）整个运动过程中，A球电势能的变化量

如图所示，匀强磁场方向水平向右，磁感应强度大小B=0.20T。正方形线圈abcd绕对称轴OO′在匀强磁场中匀速转动，转轴OO′与磁场方向垂直，线圈转速为n=120r/min。线圈的边长为L=20cm，线圈匝数N=20，线圈电阻为r=1.0Ω，外电阻R=9.0Ω，电压表为理想交流电压表，其它电阻不计，图示位置线圈平面与磁场方向平行。求线圈从图示位置转过90°过程中:

（1）所产生的平均感应电动势；
（2）通过外电阻R的电荷量q；
（3）电阻R上的电热Q；
（4）交流电压表的示数U。

如图所示，在xOy坐标系y轴右侧有垂直于纸面向里的匀强磁场，磁感应强度为B，在第四象限还有沿x轴负方向的匀强电场，y轴上有一点P，坐标已知为（0，L），一电荷量为q、质量为m的粒子从P点以某一大小未知的速度沿与y轴正方向夹角为30°的方向垂直射入磁场，已知粒子能够进入第四象限，并且在其中恰好做匀速直线运动。不计重力，求：

（1）粒子在第一象限中运动的时间t；
（2）电场强度E。

如图所示，在匀强电场和匀强磁场共存的区域内，电场的场强为E，方向竖直向下，磁场的磁感应强度为B，方向水平且垂直于纸面向里。一质量为m的带电粒子，在场区内的一竖直平面做匀速圆周运动，则可判断该带电粒子    （   ）

A．带有电量为的正电荷	B．沿圆周逆时针运动
C．运动的角速度为	D．运动的速率为

如图，A、B两球质量相等，光滑斜面的倾角为θ.图甲中A、B两球用轻弹簧相连，图乙中A、B两球用轻杆相连．系统静止时，挡板C与斜面垂直，弹簧、轻杆均与斜面平行．在突然撤去挡板的瞬间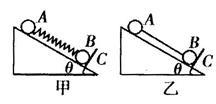

A．两图中两球加速度均为g sinθ
B．图甲中A球的加速度为零
C. 图甲中B球的加速度是为2gsinθ
D．图乙中A球的加速度为零

如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为，圆弧形轨道APD和BQC均光滑，BQC的半径为，APD的半径为，AB、CD与两圆弧形轨道相切，O₂A、O₁B与竖直方向的夹角均为.现有一质量为的小环穿在滑轨上，以某一初速度从B点开始沿AB向上运动，并恰能通过滑轨最高点.设小环与两段直轨道间的动摩擦因数均为，经过轨道连接处均无能量损失.（，，，，，，）

求：（1）小球的初速度；
（2）小球第一次到达圆弧C点时对轨道的压力；
（3）小球最后停在何处.

关于力和运动关系的说法中正确的是

A．物体所受合力的方向，就是物体的运动方向

B．物体所受合力不为零时，其速度不可能为零

C．物体所受合力不为零时，其加速度一定不为零

D．物体所受合力变小时，一定做减速运动

一转动装置如图甲所示，两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点，两轻杆与转轴间夹角均为30°，小球a、b分别套在两杆上，小环c套在转轴上，球与环质量均为m，c与a、b间均用长为L的细线相连，原长为L的轻质弹簧套在转轴上，且与轴上P点、环c相连。当装置以某一转速转动时，弹簧伸长到，环c静止在O处，此时弹簧弹力等于环的重力，球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g。求：

（1）细线刚好拉直而无张力时，装置转动的角速度ω₁
（2）如图乙所示，该装置以角速度ω₂（未知）匀速转动时，弹簧长为L/2，求此时杆对小球的弹力大小；
（3）该装置转动的角速度由ω₁缓慢变化到ω₂，求该过程外界对转动装置做的功。

甲、乙两车在平直公路上比赛，某一时刻，乙车在甲车前方L₁＝11 m处，乙车速度v_乙＝60 m/s，甲车速度v_甲＝50 m/s，此时乙车离终点线尚有L₂＝600 m，如图所示．若甲车加速运动，加速度a＝2 m/s²，乙车速度不变，不计车长，求：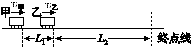

（1）经过多长时间甲、乙两车间距离最大，最大距离是多少？
（2）到达终点时甲车能否超过乙车？

如图，体积为V、内壁光滑的圆柱形导热气缸顶部有一质量和厚度均可忽略的活塞；气缸内密封有温度为2.4T₀、压强为1.2P₀的理想气体．P₀和T₀分别为大气的压强和温度．已知：气体内能U与温度T的关系为U=aT，a为正的常量；容器内气体的所有变化过程都是缓慢的．求：

（1）气缸内气体与大气达到平衡时的体积V₁；
（2）在活塞下降过程中，气缸内气体放出的热量Q．

电容式传感器是用来将各种非电信号转变为电信号的装置．由于电容器的电容C取决于极板正对面积S、极板间距离d以及极板间的电介质这几个因素，当某一物理量发生变化时就能引起上述某个因素的变化，从而又可推出另一个物理量的值的变化，如图所示是四种电容式传感器的示意图，关于这四个传感器的作用下列说法不正确的是（ ）

A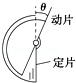． 如图的传感器可以用来测量角度

B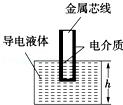． 如图的传感器可以用来测量液面的高度

C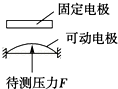． 如图的传感器可以用来测量压力

D．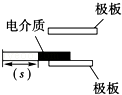

如图的传感器可以用来测量速度

如图所示，一带电平行板电容器与水平方向成37°放置，下方有绝缘挡板支撑，板间距d=2.88cm，一带正电的小球的质量为0.02g，电荷量为10^﹣7C，由电容器的中心A点静止释放恰好沿水平直线AB向右运动，从上极板边缘飞出进入边界BC右侧的水平向左的匀强电场区域，场强为2×l0³V/m，经过一段时间后发现小球打在竖直挡板C点正下方的D处，（取g=10m/s²）求：

（1）平行板电容器内的场强大小
（2）小球从上极板边缘飞出的速度
（3）CD间的距离．

如图所示，墙壁上落有两只飞镖，它们是从同一位置水平射出的。飞镖A与竖直墙壁成α角，飞镖B与竖直墙壁成β角，两者相距为d，假设飞镖的运动是平抛运动，求：

（1）射出点离墙壁的水平距离；
（2）若在该射出点水平射出飞镖C，要求它以最小动能击中墙壁，则C的初速度应为多大？
（3）在第（2）问情况下，飞镖C与竖直墙壁的夹角多大？射出点离地高度应该满足什么条件？