高中物理综合题

升降机内悬挂一圆锥摆，摆线为1m，小球质量为0.5kg，当升降机以2m/s²加速度匀加速上升时，摆线恰与竖直方向成θ=53°角，试求小球的转速和摆线的拉力大小？（g=10m/s²）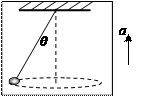

质量为10³kg的车中用细线悬挂一个质量较小的球，车在水平拉力作用下在水平公路上作直线运动，此时悬线向右偏且与竖直方向成45°角，当撤去拉力后悬线向左偏且与竖直方向成45°角，求拉力的大小和方向。（g=10m/s²）

如图所示，长为5m的细绳的两端分别系于竖立在地面上相距为4m的两杆顶端A、B.绳上挂一个光滑的轻质挂钩，其下连着一个重为12N的物体，平衡时，绳中的张力T为多少？

用细绳AC和BC吊起一重物，两绳与竖直方向的夹角如图2-2-23所示，AC能承受的最大拉力为150 N，BC能承受的最大拉力为100 N.为使绳子不断裂，所吊重物的质量不得超过多少?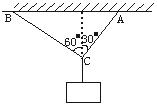

压榨机如图所示，B为固定铰链，A为活动铰链.在A处作用一水平力F，C就以比F大得多的压力D.已知L="0.5" m，h="0.1" m，F="200" N，C与左壁接触面光滑，求D受到的压力.

如图2-2-1，用轻滑轮悬挂重G的物体.绳能承受的最大拉力是2G，将A端固定，将B端缓慢向右移动d而使绳不断，求d的最大值.

如图所示，绳OC与竖直方向30°角， O为质量不计的滑轮，已知物B重1000N，物A重400N，物A、B均静止.求：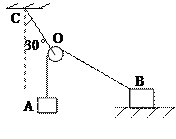

（1）物B所受摩擦力为多大？
（2）OC绳的拉力为多大？

如图所示，直线形挡板与半径为的圆弧形挡板平滑连接并安装在水平台面上，挡板与台面均固定不动。线圈的匝数为,其端点、通过导线分别与电阻和平行板电容器相连，电容器两极板间的距离为,电阻₁的阻值是线圈阻值的2倍，其余电阻不计，线圈内有一面积为、方向垂直于线圈平面向上的匀强磁场，磁场的磁感应强度随时间均匀增大。质量为的小滑块带正电，电荷量始终保持为,在水平台面上以初速度从位置出发，沿挡板运动并通过位置。若电容器两板间的电场为匀强电场，、在电场外，间距为,其间小滑块与台面的动摩擦因数为，其余部分的摩擦不计，重力加速度为.
求：
（1）小滑块通过位置时的速度大小。
（2）电容器两极板间电场强度的取值范围。
（3）经过时间,磁感应强度变化量的取值范围。

图示为修建高层建筑常用的塔式起重机。在起重机将质量=5×10³ 的重物竖直吊起的过程中，重物由静止开始向上作匀加速直线运动，加速度="0.2"，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做=1.02的匀速运动。取="10",不计额外功。求：
(1)   起重机允许输出的最大功率。
(2)   重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。

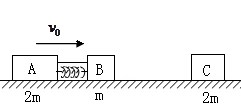
如图所示，光滑水平面轨道上有三个木块，、、，质量分别为，、用细绳连接，中间有一压缩的弹簧 (弹簧与滑块不栓接)。开始时、以共同速度运动，静止。某时刻细绳突然断开，、被弹开，然后又与发生碰撞并粘在一起，最终三滑块速度恰好相同。求与碰撞前的速度。

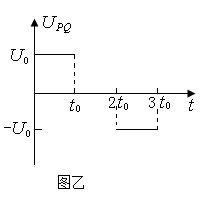
如图为一简谐波在时，对应的波形图，介质中的质点P做简谐运动的表达式为，求该波的速度，并指出时的波形图(至少画出一个波长)

一定质量的理想气体由状态经状态变为状态，其中过程为等压变化，过程为等容变化．已知，，.
(1)求气体在状态时的体积．
(2)说明过程压强变化的微观原因．
(3)设过程气体吸收热量为，过程气体放出热量为，比较、的大小并说明原因．

如图甲所示，建立坐标系，两平行极板、垂直于轴且关于轴对称，极板长度和板间距均为l，第一四象限有磁场，方向垂直于平面向里。位于极板左侧的粒子源沿轴间右连接发射质量为、电量为、速度相同、重力不计的带电粒子在时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）。
已知=0时刻进入两板间的带电粒子恰好在时，刻经极板边缘射入磁场。上述、、、、为已知量。（不考虑粒子间相互影响及返回板间的情况）
（1）求电压的大小。
（2）求时进入两板间的带电粒子在磁场中做圆周运动的半径。
（3）何时把两板间的带电粒子在磁场中的运动时间最短？求此最短时间。

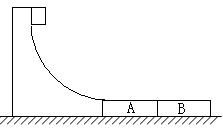
如图所示，某货场而将质量为的货物（可视为质点）从高处运送至地面，为避免货物与地面发生撞击，现利用固定于地面的光滑四分之一圆轨道，使货物中轨道顶端无初速滑下，轨道半径。地面上紧靠轨道次排放两声完全相同的木板，长度均为=2，质量均为，木板上表面与轨道末端相切。货物与木板间的动摩擦因数为，木板与地面间的动摩擦因数。（最大静摩擦力与滑动摩擦力大小相等，取=10）

（1）求货物到达圆轨道末端时对轨道的压力。
（2）若货物滑上木板4时，木板不动，而滑上木板时，木板开始滑动，求应满足的条件。
（3）若，求货物滑到木板末端时的速度和在木板上运动的时间。

如图所示，皮带传动装置与水平面夹角为30°，轮半径R= m，两轮轴心相距L=3.75m，A、B分别使传送带与两轮的切点，轮缘与传送带之间不打滑。一个质量为0.1kg的小物块与传送带间的动摩擦因数为μ= 。g取10m/s²。
（1）当传送带沿逆时针方向以v₁=3m/s的速度匀速运动时，将小物块无初速地放在A点后，它运动至B点需多长时间？（计算中可取≈16，≈20）
（2）小物块相对于传送带运动时，会在传送带上留下痕迹。当传送带沿逆时针方向匀速运动时，小物块无初速地放在A点，运动至B点飞出。要想使小物块在传送带上留下的痕迹最长，传送带匀速运动的速度v₂至少多大？