高中物理综合题

质量为m的小球由高为H的、倾角为θ光滑斜面顶端无初速滑到底端过程中，重力、弹力、合力的冲量各是多大？

目前，滑板运动受到青少年的追捧。如图是某滑板运动员在一次表演时的一部分赛道在竖直平面内的示意图，赛道光滑，为圆弧赛道，半径＝6.5，为最低点并与水平赛道位于同一水平面，、平台的高度都为＝18 。、、处平滑连接。滑板和的质量均为，＝5 ，运动员质量为，＝45 。表演开始，运动员站在滑板上，先让滑板从点静止下滑，＝0.1后再与板一起从点静止下滑。滑上赛道后，运动员从板跳到同方向运动的板上，在空中运动的时间＝0.6 。（水平方向是匀速运动）。运动员与板一起沿赛道上滑后冲出赛道，落在EF赛道的点，沿赛道滑行，经过点时，运动员受到的支持力＝742.5 。（滑板和运动员的所有运动都在同一竖直平面内，计算时滑板和运动员都看作质点，取＝10 ）

⑴滑到点时，运动员的速度是多大？
⑵运动员跳上滑板后，在赛道上与滑板共同运动的速度是多大？
⑶从表演开始到运动员滑至的过程中，系统的机械能改变了多少？

A、B两行星在同一平面内绕同一恒星做匀速圆周运动，运行方向相同，A的轨道半径为r1，B的轨道半径为r2，已知恒星质量为，恒星对行星的引力远大于得星间的引力，两行星的轨道半径r­1＜r2。若在某一时刻两行星相距最近，试求：

（1）再经过多少时间两行星距离又最近？
（2）再经过多少时间两行星距离最远？

两个星球组成双星，它们在相互之间的万有引力作用下，绕连线上某点做周期相同的匀速圆周运动。现测得两星中心距离为R，其运动周期为T，求两星的总质量。

中子星是恒星演化过程的一种可能结果，它的密度很大。现有一中子星，观测到它的自转周期为T=s。问该中子星的最小密度应是多少才能维持该星的稳定，不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.6710m/kg·s)

宇航员在一星球表面上的某高处，沿水平方向抛出一小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍，则抛出点与落地点之间的距离为L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。

2000年1月26日我国发出了一颗同步卫星。定点位置与东经98°的经线在同一平面内。若把甘肃省嘉峪关处的经度和纬度近似取为东经98°和北纬α=40°，已知地球半径R、地球自转周期T、地球表面重力加速度g（视为常量）和光速c。试求该同步卫星发出的微波信号传到嘉峪关处的接收站所需的时间（要求用题给的已知量的符号表示）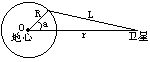

某颗地球同步卫星正下方的地球表面上有一观察者，他用天文望远镜观察被太阳光照射的此卫星，试问，春分那天（太阳光直射赤道）在日落12小时内有多长时间该观察者看不见此卫星？已知地球半径为R，地球表面处的重力加速度为g，地球自转周期为T，不考虑大气对光的折射。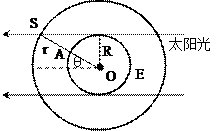

如图所示，在距一质量为M、半径为R、密度均匀的球体中心2R处，有一质量为m的质点，M对m的万有引力的大小为F。现从M中挖出一半径为r的球体，如图，OO′=R/2。求M中剩下的部分对m的万有引力的大小。

在天文学中，把两颗相距较近的恒星叫双星，已知两恒星的质量分别为m和M，两星之间的距离为L，两恒星分别围绕共同的圆心作匀速圆周运动，如图所示，求恒星运动的半径和周期。

如果某行星有一颗卫星沿非常靠近此恒星的表面做匀速圆周运动的周期为T，则可估算此恒星的密度为多少?

已知地球绕太阳公转的轨道半径r=1.491011m， 公转的周期T=3.16107s，求太阳的质量M。

如图2-11（原图2-16）所示，物体自O点由静止开始做匀加速直线运动，A、B、C、D为其轨道上的四点，测得AB=2m，BC=3m，CD=4m．且物体通过AB、BC、CD所用的时间相等，求OA间的距离．[3]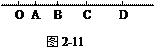

轮船在河流中逆流而上，下午7时，船员发现轮船上的一橡皮艇已失落水中，船长命令马上掉转船头寻找小艇．经过一个小时的追寻，终于追上了顺流而下的小艇．如果轮船在整个过程中相对水的速度不变，那么轮船失落小艇的时间是何时？[3 ]

甲乙两地相距220km，A车用40km/h的速度由甲地向乙地匀速运动，B车用30km/h的速度由乙地向甲地匀速运动．两车同时出发，B车出发后1h，在途中暂停2h后再以原速度继续前进，求两车相遇的时间和地点．[3 ]