如图所示，在绝缘水平面上，相距为L的A.B两点处分别固定着两个等量正电荷A.b是AB连线上两点，其中
，O为AB连线的中点，一质量为m带电量为+q的小滑块（可视为质点）以初动能
从a点出发，沿AB直线向b运动，其中小滑块第一次经过O点时的动能为初动能的2倍，到达b点时动能恰好为零，小滑块最终停在O点，求：
（1）小滑块与水平面间的动摩擦因数
。
（2）小滑块运动的总路程
。
如图所示，变阻器
的最大电阻是
，与一个规格为（6V，3W）的灯泡
串联接在电路中，电源的电动势
，当电建S闭合，变阻器的滑片在中点位置时，灯泡正常发光，设灯泡阻值恒定不变，求：（1）电源的内电阻
；（2）电源的输出功率。
如图所示，水平绝缘光滑的轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m．在轨道所在空间存在水平向右的匀强电场，电场线与轨道所在的平面平行，电场强度E=1.0×104N/C．现有一电荷量q=+1.0×10﹣4C，质量m=0.10kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体恰好能通过半圆形轨道的最高点C，然后落至水平轨道上的D点．取g=10m/s2．试求：
（1）带电体在圆形轨道C点的速度大小．
（2）PB间的距离xpB
（3）D点到B点的距离xDB．
（4）带电体在从P开始运动到落至D点的过程中的最大动能．（结果保留3位有效数字）
如图所示，汽车先向东行驶5km，又向西行驶8km，若以汽车开始运动时为坐标原点，向东为正方向，建立坐标系，试求：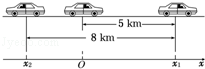
（1）汽车在最东边和最西边的位置坐标；
（2）汽车运动过程中向东的位移、向西的位移和整个过程的位移．
如图所示，在倾角为θ的粗糙斜面上，有一个质量为m的物体被水平力F推着静止于斜面上，已知物体与斜面间的动摩擦因数为μ，且μ＜tanθ，若物体恰好不下滑，则推力F为多少？若物体恰好不上滑，则推力F为多少？（最大静摩擦力等于滑动摩擦力）
1935年在苏联的一条直铁轨上，有一列火车因蒸汽不足而停驶，驾驶员把货车厢甲（如图所示）留在现场，只拖着几节车厢向前方不远的车站开进，但他忘了将货车厢刹好，使车厢在斜坡上以4m/s的速度匀速后退，此时另一列火车乙正以16m/s的速度向该货车厢驶来．驾驶技术相当好的驾驶员波尔西列夫发现货车厢甲向自己驶来时两车相距仅100m，他立即刹车，紧接着加速倒退，结果恰好接住了货车厢甲，从而避免了相撞．设列车乙刹车过程和加速倒退过程均为匀变速直线运动，且加速度大小相等，求列车乙刹车和加速倒退过程的加速度大小．
在正常情况下，火车以54km/h的速度匀速开过一个小站．现因需要，必须在这一小站停留，火车将要到达小站时，以﹣0.5m/s2的加速度做匀减速运动，停留2分钟后，又以0.3m/s2的加速度出小站，一直到恢复原来的速度．求因列车停靠小站而延误的时间．
如图所示，离地面足够高处有一竖直的空管，管长为24m，M、N为空管的上、下两端，空管受到外力作用，由静止开始竖直向下做匀加速运动，加速度为2m/s2．同时在M处一个大小不计的小球沿管的轴线竖直上抛，小球只受重力，取g=10m/s2．求：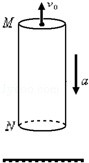
（1）若小球上抛的初速度为10m/s，经过多长时间从管的N端穿处？
（2）若此空管的N端距离地面64m高，欲使在空管到达地面时小球必须落到管内，在其他条件不变的前提下，求小球的初速度大小的范围？
如图，真空中xOy平面直角坐标系上的ABC三点构成等边三角形，边长L=2.0m，若将电荷量均为q=+2.0×10﹣6C的两点电荷分别固定在A、B点，已知静电力常量k=9.0×109N•m2/C2，求：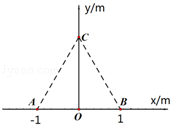
（1）两点电荷间的库仑力大小；
（2）C点的电场强度的大小和方向．
比萨斜塔是世界建筑史上的一大奇迹。如图所示，已知斜塔第一层离地面的高度h1=6.8m，为了测量塔的总高度，在塔顶无初速度释放一个小球，小球经过第一层到达地面的时间t1=0.2s，重力加速度g取10m/s2，不计空气阻力。
（1）求斜塔离地面的总高度h；
（2）求小球从塔顶落到地面过程中的平均速度
。
从离地高500 m的高空自由下落一个小球，取g="10" m/s2，求：
（1）经过多少时间落到地面；
（2）从开始下落时刻起，在第1 s内的位移，最后1 s内的位移；
（3）落下一半时间的位移.
粤公网安备 44130202000953号