如图，真空中xOy平面直角坐标系上的ABC三点构成等边三角形，边长L=2.0m，若将电荷量均为q=+2.0×10﹣6C的两点电荷分别固定在A、B点，已知静电力常量k=9.0×109N•m2/C2，求：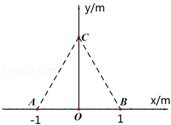
（1）两点电荷间的库仑力大小；
（2）C点的电场强度的大小和方向．
如图1所示，一质量为m的滑块（可视为质点）沿某斜面顶端A由静止滑下，已知滑块与斜面间的动摩擦因数
和滑块到斜面顶端的距离
的关系如图2所示。斜面倾角为37°，长为L。有一半径
的光滑竖直半圆轨道刚好与斜面底端B相接，且直径BC与水平面垂直，假设滑块经过B点时没有能量损失。当滑块运动到斜面底端B又与质量为m的静止小球（可视为质点）发生弹性碰撞（已知：
，
）。求：
（1）滑块滑至斜面底端B时的速度大小；
（2）在B点小球与滑块碰撞后小球的速度大小；
（3）滑块滑至光滑竖直半圆轨道的最高点C时对轨道的压力。
某同学做了用吹风机吹物体前进的一组实验，吹风机随物体一起前进时，让出气口与该物体始终保持恒定距离，以确保每次吹风过程中吹风机对物体施加的水平风力保持恒定。设物体A和物体B的质量关系
。在水平桌面上画等距的三条平行于桌子边缘的直线1、2、3，如图所示。空气和桌面对物体的阻力均忽略不计。
（1）用同一吹风机将物体按上述要求吹动A、B两物体时，获得的加速度之比；
（2）用同一吹风机将物体A从第1条线由静止吹到第2条线，又将物体B从第1条线由静止吹到第3条线。求这两次A、B物体获得的速度之比。
如图所示，质量M＝10kg、上表面光滑的足够长的木板在F＝50N的水平拉力作用下，以初速度v0="5" m/s沿水平地面向右匀速运动。现有足够多的小铁块，它们的质量均为m=1kg，将一铁块无初速地放在木板的最右端，当木板运动了L＝1m时，又无初速度地在木板的最右端放上第2块铁块，只要木板运动了L就在木板的最右端无初速度放一铁块。（取g＝10m/s2）试问：
（1）第1块铁块放上后，木板运动了L时，木板的速度多大？
（2）最终木板上放有多少块铁块？
如图所示，水平传送带AB的右端与在竖直面内的用内径光滑的钢管弯成的“9”形固定轨道相接，钢管内径很小。传送带的运行速度v0=4.0m/s，将质量m=1kg的可看做质点的滑块无初速地放在传送带的A端。已知传送带长度L= 4.0 m，离地高度h=0.4 m，“9”字全髙H= 0.6 m，“9”字上半部分3/4圆弧的半径R=0.1m，滑块与传送带间的动摩擦因数μ=0.2，重力加速度g=10 m/s2，试求：
(1)滑块从传送带A端运动到B端所需要的时间；
(2)滑块滑到轨道最高点C时对轨道作用力；
(3)滑块从D点抛出后的水平射程。
粤公网安备 44130202000953号