(12分)一匀强磁场分布在以O为圆心,半径为R的圆形区域内,方向与纸面垂直,如图所示,质量为m、电荷量q的带正电的质点,经电场加速后,以速度v沿半径MO方向进入磁场,沿圆弧运动到N点,然后离开磁场,∠MON=120º,质点所受重力不计,求:
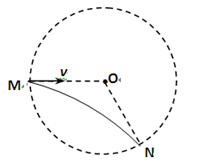
(1)判断磁场的方向;
(2)该匀强磁场的磁感应强度B;
(3)带电质点在磁场中运动的时间。
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10 27kg,电荷量q = 3.2×10 19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°= 0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
(12分)如图所示,在以等边三角形abc为边界的区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B=1T,磁场方向垂直于abc平面向里。其中等边三角形边长L= m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度
m,P、Q分别是ac、bc的中点。一带正电的粒子(不计重力)从ab边中点O沿Oc方向以速度 射入,带电粒子恰好做匀速直线运动,从c点射出。
射入,带电粒子恰好做匀速直线运动,从c点射出。
(1)求电场强度的大小和方向;
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经过t=0.5s恰好从区域的边界中点Q射出。求粒子比荷q/m的大小;
(3)若仅撤去电场,带电粒子仍从O点同方向射入,且恰好也从区域的边界另一中点P射出,求粒子速度v的大小。
如左图所示,x≥0的区域内有如右图所示大小不变、方向随时间周期性变化的磁场,磁场方向垂直纸面向外时为正方向。现有一质量为m、带电量为q的正电粒子,在t=0时刻从坐标原点O以速度v沿着与x轴正方向成75°角射入。粒子运动一段时间到达P点,P点坐标为(a,a),此时粒子的速度方向与 延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
延长线的夹角为30°.粒子在这过程中只受磁场力的作用。
(1)若B为已知量,试求粒子在磁场中运动时的轨道半径R及周期T的表达式。
(2)说明在OP间运动的时间跟所加磁场的变化周期T之间应有什么样的关系才能使粒子完成上述运动。
(3)若B为未知量,那么所加磁场的变化周期T、磁感强度B0的大小各应满足什么条件,才能使粒子完成上述运动?(写出T及B0各应满足条件的表达式)
如图甲所示,水平直线MN下方有竖直向上的匀强电场,场强E= ×10 4 N/C。现将一重力不计、比荷
×10 4 N/C。现将一重力不计、比荷 =106 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
=106 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
(1)求电荷进入磁场时的速度v0;
(2)求图乙中t=2×10-5s时刻电荷与P点的距离;
(3)如果在P点右方d=105 cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间。
如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B= 的匀强磁场中。已知匀强电场的宽度为d=
的匀强磁场中。已知匀强电场的宽度为d= R,匀强磁场由一个长为2R、宽为
R,匀强磁场由一个长为2R、宽为 R的矩形区域组成,磁场方向垂直纸面向里,粒子间的相互作用和重力均不计。
R的矩形区域组成,磁场方向垂直纸面向里,粒子间的相互作用和重力均不计。
(1)若加速电场加速电压为9U,求粒子在电磁场中运动的总时间;
(2)若加速电场加速电压为U,求粒子在电磁场中运动的总时间。
如图所示,铅盒内放有某种具有放射性的矿物,开始时其中有 、
、 两种放射性元素同位素原子核.其中
两种放射性元素同位素原子核.其中 会自发的放出某种粒子x后变成
会自发的放出某种粒子x后变成 并不再变化,
并不再变化, 发生6次α衰变和4次β衰变后变成一种稳定的原子核y.由于碰撞和其他原因,粒子x和α、β粒子从铅盒的小孔射出时的速度可以在一个很大的范围内变化.这些粒子射出后由小孔O,垂直于电场和磁场的进入一个电磁场共存的区域,其中电场强度大小E1,方向水平向左,磁感应强度大小B1,方向垂直于纸面向里.部分粒子能沿直线由小孔
发生6次α衰变和4次β衰变后变成一种稳定的原子核y.由于碰撞和其他原因,粒子x和α、β粒子从铅盒的小孔射出时的速度可以在一个很大的范围内变化.这些粒子射出后由小孔O,垂直于电场和磁场的进入一个电磁场共存的区域,其中电场强度大小E1,方向水平向左,磁感应强度大小B1,方向垂直于纸面向里.部分粒子能沿直线由小孔 射出,由A点垂直磁场、垂直于边界射入磁感应强度为B2,方向垂直纸面向里的匀强磁场中,磁场在粒子初速度方向上的宽度为d,垂直初速度方向足够大.在磁场的边界上铺有一层感光底片从
射出,由A点垂直磁场、垂直于边界射入磁感应强度为B2,方向垂直纸面向里的匀强磁场中,磁场在粒子初速度方向上的宽度为d,垂直初速度方向足够大.在磁场的边界上铺有一层感光底片从 射入的粒子最终打在1、2、3三点.设电子质量为m,电量为e,α粒子质量为7200m.求:
射入的粒子最终打在1、2、3三点.设电子质量为m,电量为e,α粒子质量为7200m.求:
(1)粒子x是什么?写出 变化成
变化成 的核反应方程;原子核y是什么?
的核反应方程;原子核y是什么?
(2)试通过计算说明打在1、2、3三点的分别是什么粒子.
(3)2点到 正对面B点的距离是多少?
正对面B点的距离是多少?
(4)若要三种粒子均不打在感光底片上,磁感应强度B2的最小值为多少?
(16 分)如图甲,距离很近的竖直边界两侧为相同的匀强磁场区域,磁场范围很大,方向垂直纸面向里。在边界上固定两个等长的平行金属板A 和D ,两金属板中心各有-小孔S1、S2 ,板间电压的变化规律如图乙,正、反向最大电压均为U0,周期为T0。一个质量为m、电荷量为+q的粒子在磁场中运动的周期也是T0 。现将该粒子在t=T0/4时刻由S1静止释放,经电场加速后通过S2又垂直于边界进人右侧磁场区域,在以后的运动过程中不与金属板相碰。不计粒子重力、极板外的电场及粒子在两边界间运动的时间。
(1)求金属板的最大长度。
(2)求粒子第n次通过S2的速度。
(3)若质量m ’="13/12" m 电荷量为+q的另一个粒子在t =" 0" 时刻由S1静止释放,求该粒子在磁场中运动的最大半径。
如图所示,在MN左侧QP上方有匀强电场。在MN右侧存在垂直于纸面的矩形匀强磁场(图中未画出),其左边界和下边界分别与MN、AA/重合。现有一带电粒子以初速度 自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d,
自O点沿水平方向射入,并恰好从P点射出,又经过在矩形有界磁场中的偏转,最终垂直于MN从A点向左水平射出。已知PA距离为d, ,
, 距离
距离 。不计带电粒子重力。
。不计带电粒子重力。
求:(1)粒子从下极板边缘射出时的速度;
(2)粒子在从O到A经历的时间
(3)矩形有界磁场的最小面积。
如图所示,磁感应强度为B方向垂直纸面向里的匀强磁场中有一粒子源,粒子源从O点在纸面内均匀地向各个方向同时发射速率为υ,比荷为k的带正电粒子.PQ是垂直纸面放置,厚度不计的挡板,挡板的P端与O点的连线跟挡板垂直,粒子打在挡板上会被吸收。带电粒子的重力及粒子间的相互作用力忽略不计,磁场分布的区域足够宽广。 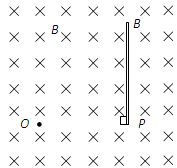
(1)为了使带电粒子不打在挡板上,粒子源到挡板的距离d应满足什么条件?
(2)若粒子源到挡板的距离d=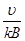 ,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。
,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。
图为可测定比荷的某装置的简化示意图,在第一象限区域内有垂直于纸面向里的匀强磁场,磁感应强度大小B,在X轴上距坐标原点L的P处为离子的入射口,在Y上安放接收器,现将一带正电荷的粒子以v的速率从P处射入磁场,若粒子在y轴上距坐标原点L的M处被观测到,且运动轨迹半径恰好最小,设带电粒子的质量为m,电量为q,不计其重力。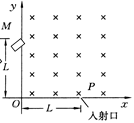
(1)求上述粒子的比荷 ;
;
(2)如果在上述粒子运动过程中的某个时刻,在第一象限内再加一个匀强电场,就可以使其沿y轴正方向做匀速直线运动,求该匀强电场的场强大小和方向;
(3)为了在M处观测到按题设条件运动的上述粒子,在第一象限内的磁场可以局限在一个矩形区域内,求此矩形磁场区域的最小面积。
如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核( Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿
Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿 方向飞离磁场,N点到O点的距离为L,已知OA间距离为
方向飞离磁场,N点到O点的距离为L,已知OA间距离为 L,α粒子质量为m,电荷量为q,氡核的质量为m0,
L,α粒子质量为m,电荷量为q,氡核的质量为m0,
(1)、写出镭核的衰变方程;
(2)、如果镭核衰变时释放的能量全部变为α粒子和氡核的动能,求一个原来静止的镭核衰变时放出的能量。
如图所示,两块平行金属极板MN水平放置,板长L =1m.间距d= m,两金属板间电压UMN = 1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为
m,两金属板间电压UMN = 1×104 V;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场B1,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上.B、C、H也处于同一直线上.AF两点距离为 m。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m = 3×10-10kg,带电量q = +1×10- 4C,初速度v0=1×105m/s。
m。现从平行金属极板MN左端沿中心轴线方向入射一个重力不计的带电粒子,粒子质量m = 3×10-10kg,带电量q = +1×10- 4C,初速度v0=1×105m/s。
(1)求带电粒子从电场中射出时的速度v的大小和方向
(2)若带电粒子进入中间三角形区域后垂直打在AC边上,求该区域的磁感应强度B1
(3)若要使带电粒子由FH边界进入FGH区域并能再次回到FH界面,求B2应满足的条件
如图所示,两块足够大的平行金属板a、b竖直放置,板间有场强为E的匀强电场,两板距离为d,今有一带正电微粒从a板下边缘以初速度v0竖直向上射入板间,当它飞到b板时,速度大小不变,而方向变为水平方向,且刚好从高度也为d的狭缝穿过b板而进入bc区域,bc区域的宽度也为d,所加电场大小为E,方向竖直向上,磁感应强度 ,方向垂直纸面向里。求:
,方向垂直纸面向里。求:
(1)微粒的带电量q;
(2)微粒穿出bc区域的位置到a板下边缘的竖直距离L(用d表示);
(3)微粒在ab、bc区域中运动的总时间t(用d、v0表示)。