高中物理电学实验综合题

如图所示为某种电子秤的原理示意图，AB为一均匀的滑线变阻器，阻值为R，长度为L，两边分别有P₁、P₂两个滑动头，与P₁相连的金属细杆可在被固定的竖直光滑绝缘杆MN上保持水平状态，金属细杆与托盘相连，金属细杆所受重力忽略不计。弹簧处于原长时P₁刚好指向A端，若P₁、P₂间出现电压时，该电压经过放大，通过信号转换后在显示屏上显示出质量的大小．已知弹簧的劲度系数为k，托盘自身质量为m₀，电源的电动势为E，电源的内阻忽略不计，信号放大器、信号转换器和显示器的分流作用忽略不计．求：
(1)托盘上未放物体时，在托盘的自身重力作用下，P₁距A端的距离x₁；
(2）在托盘上放有质量为m的物体时，P₁,距A端的距离x₂；
(3)在托盘上未放物体时通常先校准零点，其方法是：调节P₂，从而使P₁、P₂间的电压为零．校准零点后，将被称物体放在托盘上，试推导出被称物体的质量m与P₁、P₂间电压U的函数关系式．

如图所示，在磁感应强度大小为B，方向垂直纸面向里的匀强磁场中，有一个质量为m、半径为r、电阻为R的均匀圆形导线圈，线圈平面跟磁场垂直（位于纸面内），线圈与磁场边缘（图中虚线）相切，切点为A，现在A点对线圈施加一个方向与磁场垂直，位于线圈平面内并跟磁场边界垂直的拉力F，将线圈以速度v匀速拉出磁场．以切点为坐标原点，以F的方向为正方向建立x轴，设拉出过程中某时刻线圈上的A点的坐标为x.
(1)写出力F的大小与x的关系式；
(2)在F－x图中定性画出F－x关系图线，写出最大值F₀的表达式．

一个直流电动机的内电阻，与R=8的电阻串联接在线圈上，如图所示。已知线圈面积为m²，共100匝，线圈的电阻为2欧，线圈在T的匀强磁场中绕O以转速n=600r/min匀速转动时，在合上开关S后电动机正常工作时，电压表的示数为100V，求电动机正常工作时的输出功率。

如图14-18所示，R₁=R₂=R₃=1.0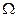，当关开S闭合时，电
压表上读数是1.0V，当开关S断开时，电压表上读数是0.8V，
求电源的电动势和内电阻。

图14-18

一个质量为m带电量为+q的小球以水平初速度v₀自h高度做平抛运动，不计空气阻力，重力加速度为g，试回答下列问题：
（1）若在空间竖直方向加一个匀强电场，发现小球水平抛出后做匀速直线运动，电场强度E是多大？
（2）撤消匀强电场后，小球再水平抛出至第一落地点P的过程，发生位移S的大小是多少？
（3）若在空间再加一个垂直纸面向外的匀强磁场，发现小球第一次落地仍然是P点，试问磁感应强度B是多大？

电磁炉专用平底锅的锅底和锅壁均由耐高温绝缘材料制成．起加热作用的是安在锅底的一系列半径不同的同心导电环(导电环的分布如图所示)．导电环所用材料每米的电阻为0.125πΩ，从中心向外第n个同心圆环的半径为＝(2n－1)r，(n＝1，2，3，…，7)，已知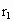＝1.0cm．当电磁炉开启后，能产生垂直于锅底方向的变化磁场，该磁场的磁感应强度B随时间的变化率为sinωt，求：

(1)半径为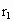的导电圆环中感应电流的最大值是多大？
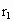(2)假设导电圆环产生的热全部以波长为1.0×m的红外线光子辐射出来，那么半径为的导电圆环上每分钟辐射出的光子数是多少？
(3)若不计其他损失，所有导电圆环释放的总功率P是多大？
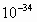(以上计算中可取＝10，h＝6.6×J·s．)

如图3-6-14所示，在倾角为30°的斜面上，固定两条无限长的平行光滑导轨，一个匀强磁场垂直于斜面向上，磁感应强度B="0.4" T，导轨间距L="0.5" m.两根金属棒ab、cd平行地放在导轨上，金属棒质量m_ab="0.1" kg,m_cd="0.2" kg，两金属棒总电阻r="0.2" Ω，导轨电阻不计.现使金属棒ab以v="1.5" m/s的速度沿斜面向上匀速运动，求: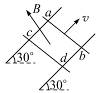

图3-6-14
（1）金属棒cd的最大速度；
（2）在cd有最大速度时，作用在金属棒ab上的外力做功的功率.

在截面积为S的粗细均匀铜导体中流过恒定电流I，铜的电阻率为ρ,电子电荷量为e，则电子在铜导体中运行时受到的电场作用力多大？

发电站发电机端电压u＝5000sin314tV，输出功率5000kW，远距离输电线的电阻为80Ω，输电线上功率损耗要求不超过总功率的4%，求:
(1)所用升压变压器的原、副线圈匝数比多大?
(2)到达用户区使用匝数比为192：1的降压变压器，对负载电阻为10Ω的用电器供电，最多可接这样的用电器几个?

一根长L=3．2 m，横截面积为S=1．6×10^-3 m²的铜棒，两端加电压U=7．0×10^-2 V.铜的电阻率ρ=1．75×10^-8 Ω·m，铜内自由电子的体积密度为n=8.5×10²⁹ m^-3.求：
（1）通过铜棒的电流；
（2）铜棒内的电场强度；
（3）自由电子定向移动的平均速率.

如图12.2-3，边长为a的正方形闭合线框ABCD在匀强磁场中绕AB边匀速转动，磁感应强度为B，初始时刻线框所在的平面与磁感线垂直，经过t时间转过120⁰角，求：（1）线框内感应电动势在时间t内的平均值。（2）转过120⁰角时感应电动势的瞬时值。

如图所示固定在匀强磁场中的正方形线框abcd，各边长为L，其中ab段是一段电阻为R的均匀电阻丝，其余三边均为电阻可忽略的铜线，磁场的磁感应强度为B，方向垂直纸面向里，现有一与ab段的材料、粗细、长度都相同的电阻丝PQ架在导线框上，以恒定的速度v从ad滑向bc，当PQ滑到何处时，通过PQ的电流最小？为多少？方向如何？

如图所示，固定在水平桌面上的光滑金属框架cdef处于竖直向下磁感应强度为的匀强磁场中．金属杆ab与金属框架接触良好．此时abed构成一个边长为l的正方形，金属杆的电阻为r，其余部分电阻不计．
(1)若从t=0时刻起，磁场的磁感应强度均匀增加，每秒的增量为是k，施加一水平拉力保持金属杆静止不动，求金属杆中的感应电流．
(2)在情况(1)中金属杆始终保持不动，当t=t₁秒末时水平拉力的大小．
(3)若从t=0时刻起，磁感应强度逐渐减小，当金属杆在框架上以恒定速度v向右做匀速运动时，可使回路中不产生感应电流．写出磁感应强度B与时间t的函数关系式．

如图14-2-7所示，相距40 km的A、B两地架两条输电线，电阻共为800 Ω，如果在A、B间的某处发生短路，这时接在A处的电压表示数为10 V，电流表示数为40 mA，求发生短路处距A有多远？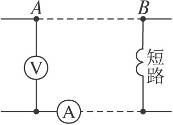

图14-2-7

如图所示，Ⅰ、Ⅲ为两匀强磁场区域，Ⅰ区域的磁场方向垂直纸面向里，Ⅲ区域的磁场方向垂直纸面向外，磁感强度为B，两区域中间为宽为s的无磁场区域Ⅱ，有一边长为L(L＞s)、电阻为R的正方形金属框abcd置于Ⅰ区域，ab边与磁场边界平行，现拉着金属框以速度v向右匀速移动。

 
(1)分别求出ab边刚进入中央无磁场区域Ⅱ和刚进入磁场区域Ⅲ时，通过ab边的电流大小和方向。
(2)把金属框从Ⅰ区域完全拉入Ⅲ区域过程中拉力所做的功。