如图所示,三个质量均为m的小木块在三个质量均为M、倾角均为α的固定锲块上下滑它们与锲块间的动摩擦因数各不相同,致使第一小木块加速下滑,第二小木块匀速下滑,第三小木块以初速υ0减速下滑.则在下滑过程中,锲块对地面的压力N1、N2、N3之间的关系为
| A.N1=N2=N3 |
| B.N1>N2>N3 |
| C.N2>N1>N3 |
| D.N3>N2>N1 |
如图所示,一轻弹簧竖直固定在地面上,上端放一质量为m的小球,小球与弹簧不拴接,平衡时弹簧被压缩x0,现用力F缓慢下压小球,使弹簧在弹性限度内再被压缩x0后撤去力F,小球立即向上弹起,上升的最大高度为4x0,重力加速度为g.在小球上升的过程中有( )

| A.小球先变加速,后变减速,再匀减速,离开弹簧时速度达到最大 |
B.小球作匀减速运动的时间为 |
| C.从小球弹起到达到最大速度的过程中克服重力做的功为2mgx0 |
| D.刚撤去力F的瞬间,小球的加速度大小为g |
如图所示,小车上固定一弯折硬杆ABC,C端固定一质量为m的小球。已知α角恒定,当小车水平向左作变加速直线运动时,BC杆对小球的作用力的方向( )
| A.一定沿着杆向上 | B.一定竖直向上 |
| C.可能水平向左 | D.随加速度a的数值的改变而改变 |
如图所示,A和B的质量分别是1 kg和2kg,弹簧和悬线的质量不计,在A上面的悬线烧断的瞬间( )
| A.A的加速度等于3g | B.A的加速度等于g |
| C.B的加速度为零 | D.B的加速度为g |
探究弹力和弹簧伸长的关系时,在弹性限度内,悬挂12 N的重物时,弹簧长度为0.16m;悬挂20 N的重物时,弹簧长度为0.20 m,则弹簧的劲度系数k为( )
| A.75 N/m | B.100 N/m | C.200 N/m | D.250 N/m |
如图所示,重物通过跨过光滑的定滑轮的轻质细绳连接到小船上,当小船匀速向左运动时(未到滑轮的正下方前),关于重物的受力及运动的说法正确的有: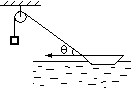
| A.重物匀速下落 |
| B.重物减速下落 |
| C.绳对重物的拉力大于重物重力 |
| D.绳对重物的拉力等于重物重力 |
在“探究弹力和弹簧伸长的关系”实验中,以下说法正确的是 ( )
| A.弹簧被拉伸时,不能超出它的弹性限度 |
| B.弹簧的弹力大小与弹簧的长度成正比 |
| C.用直尺测得弹簧的长度即为弹簧的伸长量 |
| D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比均相等. |
一本书放在水平桌面上,下列说法正确的是( )
| A.桌面受到的压力实际就是书的重力 |
| B.桌面受到的压力是由桌面形变形成的 |
| C.桌面对书的支持力与书的重力是一对平衡力 |
| D.桌面对书的支持力与书对桌面的压力一定大小相等,而且为同一性质的力 |
如图所示,弹簧秤和细绳重力不计,不计一切摩擦,物体重G=5N,弹簧秤A和B的读数分别为( )

| A.5N,0N | B.5N,10N | C.5N,5N | D.10N,5N |
如图所示为一轻质弹簧的长度l和弹力F大小的关系图象,试由图线确定: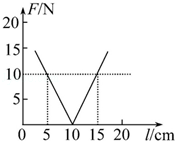
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.20m时弹力的大小.
一重为8 N的小球固定在AB杆的上端,今用测力计水平拉小球,使杆发生弯曲,如图所示,当小球达到平衡时,测力计的示数为6 N,则AB杆对小球作用力的大小为
| A.7 N | B.8 N | C.9 N | D.10 N |
如图所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中
| A.小球对墙的压力减小 |
| B.小球对薄板的压力增大 |
| C.小球对墙的压力先减小后增大 |
| D.小球对薄板的压力不可能小于球的重力 |
一物体静止在水平桌面上,则( )
| A.物体对桌面压力就是物体的重力 |
| B.桌面发生形变对物体产生支持力 |
| C.物体对桌面压力是由于桌面发生弹性形变而产生的 |
| D.压力、支持力是物体受到的一对平衡力 |
如图,物体A静止在斜面B上,下列说法正确的是( )

| A.斜面B对物块A的弹力方向是竖直向上的 |
| B.物块A对斜面B的弹力方向是竖直向下的 |
| C.斜面B对物块A的弹力方向是垂直斜面向上的 |
| D.物块A对斜面B的弹力方向跟物块A恢复形变的方向是相反的 |
如图所示,一根弹簧其自由端B在未悬挂重物时指针正对刻度5,在弹性限度内当挂上80 N重物时指针正对刻度45,若要指针正对刻度20,应挂重物是( )
| A.40 N | B.30 N | C.20 N | D.35.6N |