下列关于力的说法中正确的是 ( )
| A.只有直接接触的物体之间才会有弹力的作用 |
| B.力的大小可以用天平来直接测量 |
| C.摩擦力的方向一定与接触面相切 |
| D.重力的方向一定垂直于接触面向下 |
如图所示,用绳索将重球挂在墙上,不考虑墙的摩擦,如果把绳的长度增加一些,则球对绳的拉力F1和球对墙的压力F2的变化情况是( )

| A.F1增大,F2减小 | B.F1减小,F2增大 |
| C.F1和F2都增大 | D.F1和F2都减小 |
在倾角为α的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一中间有一圈凹槽的圆柱体,并用与斜面夹角为β的力F拉住,使整个装置处于静止状态,如图所示.不计一切摩擦,圆柱体质量为m,求拉力F的大小和斜面对圆柱体的弹力F N 的大小.

某同学分析过程如下:
将拉力F沿斜面和垂直于斜面方向进行分解.
沿斜面方向:Fcos β=mgsin α ①
沿垂直于斜面方向:Fsin β+F N =mgcos α ②
问:你同意上述分析过程吗?若同意,按照这种分析方法求出F及F N 的大小;若不同意,指明错误之处并求出你认为正确的结果.
在探究一根轻质弹簧的弹力和伸长的关系的实验中,根据测量数据作出了弹力F和弹簧的形变量x的关系图象.下列说法正确的是( )
| A.图线是经过坐标原点的曲线,说明F与x成正比 |
| B.图线是经过坐标原点的直线,说明F与x成正比 |
| C.弹簧的劲度系数与弹力成正比 |
| D.图线的斜率就是弹簧的劲度系数 |
如图所示,水平转台绕竖直轴匀速转动,穿在水平光滑直杆上的小球A和B由轻质弹簧相连并相对直杆静止.已知A、B小球的质量分别为2m和m,它们之间的距离为3L,弹簧的劲度系数为k、自然长度为L,下列分析正确的是( )
A.小球A、B受到的向心力之比为2∶1
B.小球A、B做圆周运动的半径之比为1∶2
C.小球A匀速转动的角速度为
D.小球B匀速转动的周期为
关于胡克定律的下列说法,正确的是( )
| A.拉力相同、伸长也相同的弹簧,它们的劲度系数相同 |
| B.劲度系数相同的弹簧,弹簧的伸长相同 |
| C.知道弹簧的劲度系数,就可以算出任何拉力下的弹簧伸长 |
| D.劲度系数和拉力、伸长没有关系,它只决定于弹簧的材料、长度、弹簧丝的粗细 |
如图,光滑的四分之一圆弧轨道AB固定在竖直平面内,A端与水平面相切.穿在轨道上的小球在方向始终沿轨道切线的拉力F作用下,由A向B缓慢运动,F始终沿轨道的切线方向,轨道对球的弹力为N,在运动过程中:
| A.F增大,N减小 | B.F减小,N减小 |
| C.F增大,N增大 | D.F减小,N增大 |
以下说法正确的是( )
| A.重力、弹力、动力是按力的性质来命名的 |
| B.拉力、支持力、浮力、分子力是按力的效果来命名的 |
| C.根据效果命名不同名称的力,按性质命名可能相同 |
| D.性质不同的力,对物体作用效果一定不同 |
如图所示,光滑金属球的重力G=50 N.它的左侧紧靠竖直的 墙壁,右侧置于倾角θ=37°的斜面体上.已知斜面体处于水平地面上保持静止状态,(sin 37°=3/5,cos 37°=4/5)求: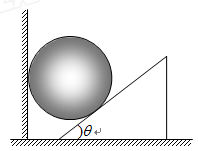
(1)墙壁对金属球的弹力大小;
(2)斜面对金属球的支持力大小.
(3)水平地面对斜面体的摩擦力的大小和方向
一个正方形木块在光滑的水平桌面上静止,下列说法正确的是( )
| A.木块对桌面的压力就是木块受的重力,施力物体是地球 |
| B.木块对桌面的压力是弹力,是由于木块发生形变而产生的 |
| C.木块受到桌面对它向上的力有弹力和支持力两个力作用 |
| D.木块保持静止是由于木块对桌面的压力与桌面对木块的支持力二力平衡 |
在“探究弹力和弹簧伸长的关系”实验中,以下说法正确的是 ( )
| A.弹簧被拉伸时,不能超出它的弹性限度 |
| B.弹簧的弹力大小与弹簧的长度成正比 |
| C.用直尺测得弹簧的长度即为弹簧的伸长量 |
| D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比均相等. |
一本书放在水平桌面上,下列说法正确的是( )
| A.桌面受到的压力实际就是书的重力 |
| B.桌面受到的压力是由桌面形变形成的 |
| C.桌面对书的支持力与书的重力是一对平衡力 |
| D.桌面对书的支持力与书对桌面的压力一定大小相等,而且为同一性质的力 |
如图所示,弹簧秤和细绳重力不计,不计一切摩擦,物体重G=5N,弹簧秤A和B的读数分别为( )

| A.5N,0N | B.5N,10N | C.5N,5N | D.10N,5N |
如图所示为一轻质弹簧的长度l和弹力F大小的关系图象,试由图线确定: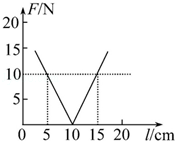
(1)弹簧的原长;
(2)弹簧的劲度系数;
(3)弹簧长为0.20m时弹力的大小.