如图,两个相同的弹性小球,分别挂在不能伸长的细绳上,开始时两绳互相平行,两球在同一水平线上且互相接触,第二球的摆长是第一球摆长的 4 倍。现把第一球拉开一个很小的角度后释放并开始计时,则在第一个摆球固有周期的两倍时间内,两球碰撞的次数为 ( )

| A.2次 | B.3次 |
| C.4次 | D.5次 |
单摆的周期在下述情况下会变大的有:()
| A.摆锤质量增大 |
| B.摆长减小 |
| C.单摆从赤道移到北极 |
| D.单摆从海平面移到高山 |
如图所示,A、B为固定在轻杆中点和一个端点的两个小球,杆可绕O点无摩擦地转动,将轻杆从图中水平位置由静止释放,在轻杆下落到竖直位置的过程中( )

A、两球各自的机械能均守恒
B、杆、球组成的系统机械能守恒
C、A球机械能的增加等于B球机械能的减少
D、A球机械能的减少等于B球机械能的增加
一个单摆,如果摆球的质量增加为原来的4倍,摆球经过平衡位置时速度减为原来的1/2则单摆的( )
| A.频率不变,振幅不变 |
| B.频率不变,振幅改变 |
| C.频率改变,振幅不变 |
| D.频率改变,振幅改变 |
火车在恒定功率下由静止出发,沿水平轨道行驶,5 min后速度达到最大20m/s,若火车在运动过程中所受阻力大小恒定。则该火车在这段时间内行驶的距离:( )
| A.可能等于3km | B.一定大于3km |
| C.一定小于3km | D.无法确定 |
如图所示,质量mA为4.0kg的木板A放在水平面C上,木板与水平面间的动摩擦因数μ为0.24,木板右端放着质量mB为1.0kg的小物块B(视为质点),它们均处于静止状态.木板突然受到水平向右的12N·s的瞬时冲量作用开始运动,当小物块滑离木板时,木板的动能EKA为8.0J,小物块的动能EKB为0.50J,重力加速度取10m/s2,求: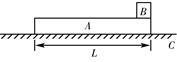
(1)瞬时冲量作用结束时木板的速度υ0;
(2)木板的长度L.
质量为M的小车中挂有一个单摆,摆球的质量为M0,小车和单摆以恒定的速度V0沿水平地面运动,与位于正对面的质量为M1的静止木块发生碰撞,碰撞时间极短,在此过程中,下列哪些说法是可能发生的( )
| A.小车、木块、摆球的速度都发生变化,分别为V1、V2和V3,且满足:(M+M0)V0=MV1+M1V2+M0V3; |
| B.摆球的速度不变,小车和木块的速度为V1、V2,且满足:MV0=MV1+M1V2; |
| C.摆球的速度不变,小车和木块的速度都为V,且满足:MV0=(M+M1)V; |
| D.小车和摆球的速度都变为V1,木块的速度变为V2,且满足:(M+M0)V0=(M+M0)V1+M1V2 |
运输货车的制造标准是:当汽车侧立在倾角为30°的斜坡上时,如图1-4(原图1-17)所示,仍不致于翻倒,也就是说,货车受的重力的作用线仍落在货车的支持面(以车轮为顶点构成的平面范围)以内.如果车轮间的距离为2.0m,车身的重心离支持面不超过多少?(设车的重心在如图所示的中轴线上)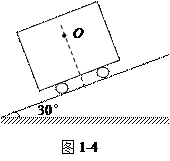
如图所示,为一轻质弹簧的长度和弹力大小的关系.根据图象判断,正确的结论是 ( )
| A.弹簧的劲度系数为1 N/m |
| B.弹簧的劲度系数为100 N/m |
| C.弹簧的原长为6 cm |
| D.弹簧伸长0.2 m时,弹力的大小为4 N |

探究弹力和弹簧伸长的关系时,在弹性限度内,悬挂15N重物时,弹簧长度为0.16m;悬挂20N重物时,弹簧长度为0.18m,则弹簧的原长L原和劲度系统k分别为( )
| A.L原=0.02m k=500N/m |
| B.L原=0.10m k=500N/m |
| C.L原=0.02m k=250N/m |
| D.L原=0.10m k=250N/m |
关于物体的重心,下列说法中正确的是()
| A.任何物体的重心都一定在这个物体上 |
| B.重心的位置只与物体的形状有关 |
| C.形状规则、质量分布均匀的物体,其重心在物体的几何中心 |
| D.物体重心的位置一定会随物体形状改变而改变 |