高中物理力学实验试题

一转动装置如图甲所示，两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点，两轻杆与转轴间夹角均为30°，小球a、b分别套在两杆上，小环c套在转轴上，球与环质量均为m，c与a、b间均用长为L的细线相连，原长为L的轻质弹簧套在转轴上，且与轴上P点、环c相连。当装置以某一转速转动时，弹簧伸长到，环c静止在O处，此时弹簧弹力等于环的重力，球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内，忽略一切摩擦和空气阻力，重力加速度为g。求：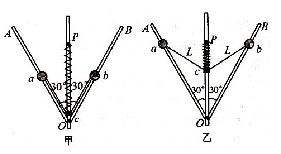

（1）细线刚好拉直而无张力时，装置转动的角速度ω₁
（2）如图乙所示，该装置以角速度ω₂（未知）匀速转动时，弹簧长为L/2，求此时杆对小球的弹力大小；
（3）该装置转动的角速度由ω₁缓慢变化到ω₂，求该过程外界对转动装置做的功。

水平地面上的物体受重力G和水平作用力F保持静止，如图所示，现在使作用力F保持大小不变，方向沿逆时针方向缓慢转过180⁰，而物体始终保持静止，则在这个过程中，物体对地面的正压力F_N和地面给物体的摩擦力F_f的变化情况是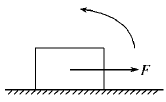

A．Ff不变

B．Ff先变小后变大

C．FN先变小后变大

D．FN先变大后变小

如图，质量的两物体A、B叠放在一起放在倾角为的光滑斜面上，现让它们由静止开始释放，在沿斜面下滑过程中，物体B的受力图是（  ）

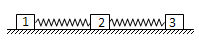
如图所示，在水平面上有三个质量分别为m₁，m₂，m₃的木块，木块1和2、2和3间分别用一原长为L、劲度系数为K的轻弹簧连接起来，木块1、2与水平面间的动摩擦因数为μ，木块3和水平面之间无摩擦力．现用一水平恒力向右拉木块3，当木块一起匀速运动时，1和3两木块间的距离为（木块大小不计）（  ）

A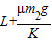．	B．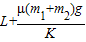
C．	D．

如图，在光滑的倾角为θ的固定斜面上放一个劈形的物体A，其上表面水平，质量为M．物体B质量为m，B放在A的上面，先用手固定住A．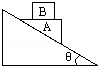

（1）若A的上表面粗糙，放手后，求AB相对静止一起沿斜面下滑，B对A的压力大小．
（2）若A的上表面光滑，求放手后的瞬间，B对A的压力大小．

木块A的质量m_A=3kg、木板m_B=1.5kg木板B两面平行，放在倾角为37°的三角体C上．木块A被一根固定在天花板上的轻绳拉住，绳拉紧时与斜面的夹角也是37°．已知A与B，B与C之间的动摩擦因数均为μ=1/3．现用平行于斜面的拉力F将木板B从木块A下面匀速抽出，同时C保持静止．（重力加速度g取10m/s2，sin37°=0.6，cos37°=0.8），求：

（1）绳子对A木块的拉力大小；
（2）拉力F的大小；

如图所示，轻质弹簧的劲度系数为20 N/cm，用其拉着一个重200 N的物体在水平面上运动．当弹簧的伸长量为4 cm时，物体恰在水平面上做匀速直线运动．
 
（1）求物体与水平面间的动摩擦因数；
（2）当弹簧的伸长量为6 cm时，物体受到的水平拉力有多大？这时物体受到的摩擦力有多大？
（3）如果在物体运动的过程中突然撤去弹簧，而物体在水平面上能继续滑行，这时物体受到的摩擦力有多大？

某物理小组的同学设计了一个粗制玩具小车通过凹形桥最低点的速度的实验，所用器材有：玩具小车、压力式托盘秤、凹形桥模拟器（圆弧部分的半径为R=0.20m）。完成下列填空：
将凹形桥模拟器静置于托盘秤上，如图（a）所示，托盘秤的示数为1.00kg；
将玩具车静置于凹形桥模拟器最低点时，托盘秤的示数如图b所示，该示数为______kg；
将小车从凹形桥模拟器某一位置释放，小车经过最低点后滑向另一侧，此过程中托盘秤的最大示数为m；多次从同一位置释放小车，记录各次的m值如下表所示：

序号	1	2	3	4	5
m（kg）	1.80	1.75	1.85	1.75	1.90

 
根据以上数据，可求出小车经过凹形桥最低点时对桥的压力为____N；小车通过最低点时的速度大小为______m/s。（重力加速度，计算结果保留2位有效数字）。

如图所示，不带电物体A和带电的物体B用跨过定滑轮的绝缘轻绳连接，A、B的质量分别是2m和m.劲度系数为k的轻质弹簧一端固定在水平面上，另一端与物体A相连，倾角为θ的绝缘斜面处于沿斜面向上的匀强电场中.开始时，物体B受到沿斜面向上的外力F=3mgsinθ的作用而保持静止，且轻绳恰好伸直.现撤去外力F，直到物体B获得最大速度，且弹簧未超过弹性限度，不计一切摩擦.则在此过程中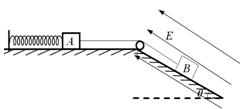

A.B的速度最大时，弹簧的伸长量为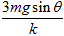
B.物体B所受电场力大小为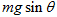
C.撤去外力F的瞬间，物体B的加速度为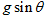
D.物体A、弹簧和地球组成的系统机械能增加量等于物体B和地球组成的系统机械能的减少量

如图所示，ABCD竖直放置的光滑绝缘细管道，其中AB部分是半径为R的圆弧形管道，BCD部分是固定的水平管道，两部分管道恰好相切于B。水平面内的M、N、B三点连线构成边长为L等边三角形，MN连线过C点且垂直于BCD。两个带等量异种电荷的点电荷分别固定在M、N两点，电荷量分别为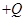和。现把质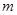量为、电荷量为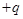的小球（小球直径略小于管道内径，小球可视为点电荷），由管道的A处静止释放，已知静电力常量为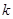，重力加速度为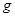。求：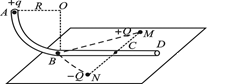

（1）小球运动到B处时受到电场力的大小；
（2）小球运动到C处时的速度大小；
（3）小球运动到圆弧最低点B处时，小球对管道压力的大小。

如图所示，质量为M、半径为R的半球形物体A静止在粗糙水平地面上，通过最高点处的钉子用水平轻质细线拉住一质量为m、半径为r的光滑球B，重力加速度为g。则（    ）

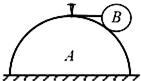
A．A对地面的摩擦力方向向左

B．B对A的压力大小为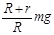

C．细线对小球的拉力大小为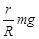

D．若剪断绳子（A不动）,则此瞬时球B加速度大小为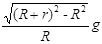

如图，在水平轨道右侧固定半径为R的竖直圆槽形光滑轨道，水平轨道的PQ段铺设特殊材料，调节其初始长度为l，水平轨道左侧有一轻质弹簧左端固定，弹簧处于自然伸长状态．可视为质点的小物块从轨道右侧A点以初速度v₀冲上轨道，通过圆形轨道、水平轨道后压缩弹簧，并被弹簧以原速率弹回．已知R=0.4m，l=2.5m，v₀=6m/s，物块质量m=1kg，与PQ段间的动摩擦因数μ=0.4，轨道其它部分摩擦不计．取g=10m/s²．求：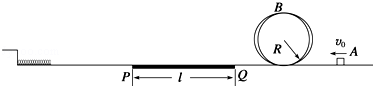

（1）物块经过圆轨道最高点B时对轨道的压力；
（2）物块从Q运动到P的时间及弹簧获得的最大弹性势能；
（3）物块仍以v₀从右侧冲上轨道，调节PQ段的长度l，当l长度是多少时，物块恰能不脱离轨道返回A点继续向右运动．

一个重30N的物体置于斜面上，如图，斜面的倾斜角为30°，挡板竖直，不计一切摩擦．（取g=10m/s²）

（1）画出小球受力分析示意图．
（2）求出斜面和挡板对小球的作用力．

下列说法正确的是（ ）

A．弹力的方向不一定与接触面垂直

B．两物体间的滑动摩擦力总是与物体运动方向相反

C．摩擦力的大小与弹力成正比

D．两分力大小一定，夹角越小，合力越大

如图所示，质量为10kg的物体A拴在一个被水平拉伸的弹簧一端，弹簧的拉力为5N时，物体A和小车均处于静止状态．若小车以1m/s²的加速度向右加速运动后，则（g=10m/s²）

A．物体A相对小车向左运动

B．物体A受到的摩擦力减小

C．物体A受到的摩擦力大小不变

D．物体A受到的弹簧拉力增大