高中物理力学实验综合题

1、经检测汽车A的制动性能：以标准速度20m/s，在平直公路上行驶时，制动后40s停下来。现A在平直公路上以20m/s的速度行驶，发现前方180m处有一货车B以6m/s的速度同向匀速行使，因该路段只能通过一个车辆，司机立即制动，
关于能否发生撞车事故，某同学的解答过程是：
“设汽车A制动后40s的位移为S₁，货车B在这段时间内的位移为S₂.则：
A车的位移为：
B车的位移为：
两车位移差为400-240=160（m）<180（m）；两车不相撞。”
你认为该同学的结论是否正确？如果你认为正确，请定性说明理由；如果你认为不正确，请说明理由并求出正确结果。

空间探测器从行星旁绕过，由于行星的作用，可以使探测器的运动速率增大，这种现象被称为“弹弓效应”。在航天技术中，“弹弓效应”是用来增大人造小天体运动速率的一种有效方法。1989年10月发射的伽利略探测器就曾利用这种效应。土星的质量M=5.67×1026 kg ，以相对太阳的轨道速率u0="9.6" km/s 运行；伽利略空间探测器的质量为m="150" kg ，相对于太阳迎向土星的速率为v0="10.4" km/s ，由于“弹弓效应”探测器绕过土星后，沿与原来速度相反的方向离去，求它离开土星后相对于太阳的速率。

如图所示，在水平地面上有A、B两个小物体，质量分别为m_A＝3.00 kg、m_B＝2.00 kg，它们与地面间的动摩擦因数均为μ＝0.1.A、B之间有一原长为L＝15.0 cm、劲度系数为k＝500 N/m的轻质弹簧连接。分别用两个方向相反的水平恒力F₁、F₂同时作用在A、B两物体上。当运动达到稳定时，A、B两物体以共同加速度大小为a＝1.00 m/s²做匀加速运动。已知F₁＝20.0 N，g取10 m/s²。求：运动稳定时A、B之间的距离。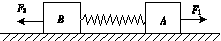

如图甲所示，一质量为2 . 0kg 的物体静止在水平面上，物体与水平面间的动摩擦因数为0.20。从t = 0时刻起，物体受到水平方向的力F 的作用而开始运动， 8s内F随时间t 变化的规律如图乙所示。求：（g取 10m / s ²）

（1）4s末物体速度的大小；
（2）在图丙的坐标系中画出物体在8s内的v-t 图象；（要求计算出相应数值）
（3）在8s 内水平力F所做的功。

粮食存储仓库常常需要利用倾斜的传送带将装满粮食的麻袋运送到高处，如图所示。已知某粮仓的传送带长15m，与水平面的夹角为30º，在电动机的带动下，传送带以0.3m/s的恒定速率向斜上方运送麻袋。电动机的最大输出机械功率为10kw，传送装置本身消耗的功率为4.0kw。设每个麻袋的总质量为90kg，传送带的移动速率保持不变，并设将麻袋放在传送带上时麻袋具有与传送带相同的速度，g取10m/s²。
（1）麻袋被传送带从最底端运送到顶端的过程中，传送带对每个麻袋做的功为多少？
（2）该传送带每分钟最多能运送麻袋多少个？

如图 10 所示，质量m =" 2kg" 的物体静止在水平地面上，物体与地面间的动摩擦因数μ = 0.75。一个与水平方向成 37°角斜向上、大小F =" 20N" 的力拉物体，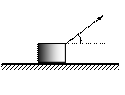

使物体匀加速运动，2s后撤去拉力. 求物体在整个过程中发生的位移？ （sin37°= 0.6，cos37°= 0.8，g =" 10" m/s²）

、图（1）表示用水平恒力F拉动水平面上的物体，使其做匀加速运动。当改变拉力的大小时，相对应的匀加速运动的加速度a也会变化，a和F的关系如图（2）所示。

（1）该物体的质量为多少？
（2）在该物体上放一个与该物体质量相同的砝码，保持砝码与该物体相对静止，其他条件不变，请在图2的坐标上画出相应的a——F图线。
（3）由图线还可以得到什么物理量？（要求写出相应的表达式或数值）

（1）如图，在水平地面上固定一个内侧长为L、质量为M的薄壁箱子。光滑的物块B的质量为m，长为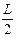，其左端有一光滑小槽，槽内装有轻质弹簧。开始时，使B紧贴A₁壁，弹簧处于压缩状态，其弹性势能为E_p。现突然释放弹簧，滑块B被弹开。假设弹簧的压缩量较小，恢复形变所用的时间可以忽略。求滑块B到达A₂壁所用的时间。
（2）a．现将箱子置于光滑的水平地面上而不固定，仍使B紧贴A₁壁，弹簧处于压缩状态，其弹性势能为E_p，整个系统处于静止状态。现突然释放弹簧，滑块B离开A₁壁后，弹簧脱落并被迅速拿出箱子。求此时滑块B的速度v与箱子的速度V。
b．假设滑块B与A₁壁和A₂壁的碰撞过程中无机械能损失。试定量描述滑块B相对于地面运动的速度变化情况，并计算两次碰撞之间的时间间隔。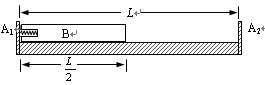

（1）在这一过程中电动机要消耗的电能E₁；  
（2）一袋水泥机械能的增加量E₂； 
（3）摩擦所产生热量Q；           

跳伞运动员做低空跳伞表演，直升飞机离地面高度H=224m静止在空中，运动员离开飞机在竖直方向做自由落体运动；经过一段时间后，立即打开降落伞，展开伞后运动员以a=12.5m/s²的加速度在竖直方向上匀减速下降，若运动员落地时竖直方向的速度为v=5m/s，(g=lOm/s²)求：
(1)运动员展开伞时，离地面的高度h?
(2)运动员在空中运动时间t?

如图所示，在空间中的A、B两点固定着一对等量正点电荷，有一带电微粒在它们产生的电场中运动，设带电微粒在运动过程中只受到电场力的作用，带电微粒在电场中所做的运动可能是：A．匀变速直线运动、B．匀速圆周运动、C．类似平抛运动、D．机械振动。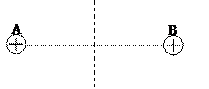

现有某同学分析如下：带电粒子在电场中不可能做匀变速直线运动与类似平抛运动，因为带电粒子在电场中不可能受到恒定的外力作用，所以A、C是错误的，也不可能做匀速圆周运动，因为做匀速圆周运动的物体所受的合外力始终指向圆心充当向心力，图示中两点电荷所产生的电场不可能提供这样的向心力，所以B也是错误的。唯有D正确，理由是在AB连线中点O两侧对称位置之间可以做机械振动。
你认为该同学的全部分析过程是否有错，若没有错，请说明正确答案“D”成立的条件？若有错，请指出错误并说明理由。

推行节水工程的转动喷水“龙头”如图所示，“龙头”距地面h，可将水水平喷出，其喷灌半径可达10h。每分钟喷水mkg，所用的水是从地下H深的井里抽取。设水以相同的速率喷出。水泵效率为η，不计空气阻力，试求：
（1）水从喷水“龙头”喷出的初速度
（2）水泵每分钟对水做的功
（3）带动水泵的电动机的最小输出功率

如图所示，将一根光滑的细金属棒折成V形，顶角为2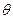，其对称轴竖直，在其中一边套上一个质量为m的小金属环P，
（1）若固定V形细金属棒，小金属环P从距离顶点O为x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O点时需多少时间？
（2）若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动时，则小金属环离对称轴的距离为多少？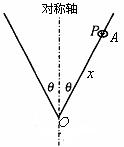

如图所示，光滑水平地面上停着一辆平板车，其质量为，长为L，车右端（A点）有一块静止的质量为的小金属块．金属块与车间有摩擦，与中点C为界， AC段与CB段动摩擦因数不同．现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，即撤去这个力．已知撤去力的瞬间，金属块的速度为，车的速度为，最后金属块恰停在车的左端（B点）。如果金属块与车的AC段间的动摩擦因数为，与CB段间的动摩擦因数为，求与的比值．

A、B两球质量分别为和，用一劲度系数为的弹簧相连，一长为的细线与相连，置于水平光滑桌面上，细线的另一端拴在数值轴上，如图所示。当与均以角速度绕做匀速圆周运动且稳定后，弹簧长度为。求：
（1）此时绳子的张力大小。
（2）将线突然烧断的瞬间，A球的加速度是多大？