(1)要使盒子在最高点时盒子与小球之间恰好无作用力，则该盒子做匀速圆周运动的周期为多少？
(2)若盒子以第（１）问中周期的
做匀速圆周运动，则当盒子运动到图示球心与O点位于同一水平面位置时，小球对盒子的哪些面有作用力，作用力为多大？
如图所示，用一根长为l＝1m的细线，一端系一质量为m＝1kg的小球（可视为质点），另一端固定在一光滑锥体顶端，锥面与竖直方向的夹角θ＝37°，当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时，细线的张力为T。求（取g＝10m/s2，结果可用根式表示）：
（1）若要小球离开锥面，则小球的角速度ω0至少为多大？
（2）若细线与竖直方向的夹角为60°，则小球的角速度ω＇为多大？
（3）细线的张力T与小球匀速转动的加速度ω有关，请在坐标纸上画出ω的取值范围在0到ω＇之间时的T—ω2的图象（要求标明关键点的坐标值）。
如图所示，可视为质点的三物块A、B、C放在倾角为300、长L=2m的固定斜面上，物块与斜面间的动摩擦因数μ＝
，A与B紧靠在一起，C紧靠在固定挡板上，三物块的质量分别为mA＝0.80kg、mB＝0.64kg、mC＝0.50kg，其中A不带电，B、C的带电量分别为qB＝＋4.0×10-5C、qC＝＋2.0×10-5C且保持不变，开始时三个物块均能保持静止且与斜面间均无摩擦力作用。如果选定两点电荷在相距无穷远处的电势能为零，则相距为r时，两点电荷具有的电势能可表示为
。现给A施加一平行于斜面向上的力F，使A在斜面上一直作加速度a＝1.5m/s2的匀加速直线运动，经过时间t0，力F变为恒力，当A运动到斜面顶端时撤去力F。已知静电力常量k＝9.0×109N·m2／C2，g＝10m/s2。求：
（1）未施加力F时物块B、C间的距离；
（2）t0时间内A上滑的距离；
（3）力F对A物块做的总功。
如图所示，斜面倾角为45°，从斜面上方A点处由静止释放一个质量为m的弹性小球，在B点处和斜面碰撞，碰撞后速度大小不变，方向变为水平，经过一段时间在C点再次与斜面碰撞。已知AB两点的高度差为h，重力加速度为g，不考虑空气阻力。求：
（1）小球在AB段运动过程中重力做功的平均功率P；
(2)小球落到C点时速度的大小。
“神舟六号”载人飞船在发射初期，宇航员的血液处于超重状态，严重时会产生黑视，甚至危及生命。
（1）假设载人飞船起飞时视为匀加速直线运动，加速度大小为60m/s2，方向竖直向上，两名宇航员在飞船内是躺在水平躺椅上的，则他们对躺椅的压力约为其重力的多少倍？（g=10m/s2）
（2）为了宇航员适应上述情况，必须进行专门的训练。训练的装置是半径为20m的水平坐舱，在电力的驱动下坐舱在水平面内做匀速圆周运动，若让坐舱在运动中的加速度大小为80m/s2，则坐舱每分钟应转动多少圈？（π约取3）
如下图所示，在半径R＝20cm、质量M＝168kg的均匀铜球中，挖去一球形空穴，空穴的半径为要，并且跟铜球相切，在铜球外有一质量m＝1kg、体积可忽略不计的小球，这个小球位于连接铜球球心跟空穴中心的直线上，并且在空穴一边，两球心相距是d＝2m，试求它们之间的相互吸引力． 
一只蚂蚁从蚂蚁洞沿直线爬出，已知爬出速度v的大小与距蚂蚁洞中心的距离L成反比，当蚂蚁到达距蚂蚁洞中心的距离L1=1m的A点时，速度大小为v1=20cm/s，问当蚂蚁到达距蚂蚁洞中心的距离L2=2m的B点时，其速度大小为v2="?" 蚂蚁从A点到达B点所用的时间t=?
如图所示，在足够长的光滑水平轨道上静止三个小木块A、B、C，质量分别为mA=1kg，
mB=1kg，mC=2kg，其中B与C用一个轻弹簧固定连接，开始时整个装置处于静止状态；A和B之间有少许塑胶炸药，A的左边有一个弹性挡板（小木块和弹性挡板碰撞过程没有能量损失）．现在引爆塑胶炸药，若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能，A和B分开后，A恰好在B、C之间的弹簧第一次恢复到原长时追上B，并且与B发生碰撞后粘在一起．求：
（1）在A追上B之前弹簧弹性势能的最大值；
（2）A与B相碰以后弹簧弹性势能的最大值．
质量分别为m1和m2的两个小物块用轻绳连接，绳跨过位于倾角＝30°的光滑斜面顶端的轻滑轮，滑轮与转轴之间的摩擦不计，斜面固定在水平桌面上，如图所示。第一次，m1悬空，m2放在斜面上，用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间。第二次，将m1和m2位置互换，使m2悬空，m1放在斜面上，发现m1自斜面底端由静止开始运动至斜面顶端所需的时间为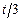
。求m1与m2之比。
粤公网安备 44130202000953号
