高中物理力学实验实验题

质量为2㎏的物体，静止于水平面上，从t = 0时刻开始对物体施加水平力F₁和竖直向下的力F₂的作用。已知F₁=" 6" t (N)、F₂ = 4 t (N)，水平面对物体的最大静摩擦力等于压力的0.5倍，那么，t =1s时，物体受到的摩擦力大小为_______N；t =______s时，物体开始运动。（取g =10m/s²）

画出图中小球和杆所受的力的示意图（接触面光滑），请在答卷纸上直接画出示意图

在《用单摆测定重力加速度》的实验中：
（1）某同学用秒表测得单摆完成40次全振动的时间如图(a)所示，则单摆的周期为       s。

（2）实验中对提高测量结果精度有利的建议是______。

A．单摆的摆线不能太短

B．单摆的摆球密度尽可能大

C．单摆的摆角越大越好

D．从平衡位置开始计时，测量一次全振动的时间作为摆动周期

（3）若单摆在任意摆角θ时的周期公式可近似为T=T₀[1+asin²(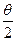)]，式中T₀为摆角趋近于0°时的周期，a为常数；为了用图象法验证该关系式，需要测量的物理量有________；某同学在实验中得到了如图(b)所示的图线，则图线的斜率表示_______。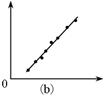

一位同学做“探究形变与弹力的关系”的实验。下列的实验步骤是这位同学准备完成的，请你帮这位同学按操作的先后顺序，用字母排列出来是      。

A．以弹簧伸长量为横坐标，以弹力为纵坐标，描出各组数据（x，F）对应的点，并用平滑的曲线连结起来；

B．记下弹簧不挂钩码时，其下端在刻度尺上的刻度L0；

C．将铁架台固定于桌子上，并将弹簧的一端系于横梁上，在弹簧附近竖直固定一刻度尺；

D．依次在弹簧下端挂上1个、2个、3个、4个……钩码，并分别记下钩码静止时，弹簧下端所对应的刻度并记录在表格内，然后取下钩码；

E、以弹簧伸长量为自变量，写出弹力与弹簧伸长量的关系式；

利用单摆测重力加速度的实验中，如果偏角足够小，但测出的重力加速度的数值偏大，可能原因是                                        （   ）

A．振幅较小

B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心

C．数振动次数时，少计了一次

D．数振动次数时，多计了一次

某兴趣小组想要探究单摆的周期T与摆长、摆球质量m的关系：
（1）为了探究周期T与摆长、摆球质量m的关系，应利用_________法完成此实验；为了准确测量单摆的周期，应使摆球振动稳定后且经过_________位置开始计时。
（2）他们在探究周期T与摆长的关系时，测得如下5组数据，请在图中选择恰当坐标，作出直观反映周期T与摆长关系的图像。

数值   　　　　次数 项目	1	2	3	4	5
	1.78	1.90	1.99	2.10	2.19
（）	3.19	3.60	3.99	4.40	4.79
（）	0.80	0.90	1.00	1.10	1.20
（）	0.64	0.81	1.00	1.21	1.44

（3）根据图像求得当地的重力加速度g=___________m/s²。（保留三位有效数字）
（4）某学生做实验时固定好装置后先测摆长，然后测出周期，发现测得的重力加速度偏大，原因可能是______（填选项前字母）

A．单摆的悬点未固定紧，振动中出现松动，使摆线增长了

B．把摆球n次经过最低点的时间误记为(n + 1)次经过最低点的时间

C．计时结束时，秒表过早按下

D．单摆所用摆球质量过大

（1）某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.50cm；摆球直径为2.00 cm；然后用秒表记录了单摆振动50次所用的时间为99.9s．则
①该摆摆长为_______cm，周期为       s
②如果他测得的g值偏小，可能的原因是 [   ]

A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时，秒表过迟按下	D．实验中误将49次全振动数为50次

（2）在一次用单摆测定加速度的实验中，图A的O点是摆线的悬挂点，a、b点分别是球的上沿和球心，摆长L=      m. 秒表读数__________
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T²为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T²与L的关系图线.

在研究匀变速直线运动的实验中，如图所示为一次记录小车运动情况的纸带，图中A、B、C、D、E为相邻的计数点，相邻计数点间的时间间隔为T=0.1s.

（1）根据_______可判定小球做__________运动；
（2）计算C点速度v_C=_____m/s；
（3）根据纸带点的分布，求出加速度a=_________m/s²；

用单摆测重力加速度时
（1）摆球应采用直径较小,密度尽可能_____的球,摆线长度要在1米以上,用细而不易______的尼龙线；
（2）摆线偏离竖直方向的角度θ应_______；
（3）要在摆球通过________位置时开始计时,摆线每经过此位置______次才完成一次全振动；
（4）摆球应在________面内摆动,每次计时时间内,摆球完成全振动次数一般选为___      ____次。利用单摆测重力加速度的实验中，摆长的测量应在摆球自然下垂的状况下从悬点量至                。某同学组装了如图所示的单摆，并用图示的L作为摆长，这样测得的g值将偏     。（填“大”或“小”）

有一秒摆T="2" s，摆球的质量为0.04 kg，当摆球质量增加到0.08 kg时，它的周期是_______，当摆长增加到原来的4倍时，它的振动频率是_________。

一个秒摆摆球的质量为0.2 kg，它振动到最大位移时距最低点的高度为0.4 cm，它完成10次全振动回到最大位移时，距最低点的高度变为0.3 cm，如果每完成10次全振动给它补充一次能量，使摆球回到原来的高度，在60 s内总共补充的能量是____________________.

在“用单摆测定重力加速度”的实验中，用刻度尺测量悬点到小球的距离为96.60 cm，用卡尺量得小球直径是5.260 cm，测量周期有3次，每次是在摆球通过最低点时，按下秒表开始计时，同时将此次通过最低点作为第一次，接着一直数到计时终止，结果如下表.

	1	2	3
数的次数	61	81	71
时间（s）	60.40	79.80	70.60

这个单摆振动周期的测定值是_______________s，当地重力加速度的值是__________m/s².（取三位有效数字）

将在地球上校准的摆钟拿到月球上去，若此钟在月球记录的时间是1 h，那么实际的时间应是______________h(月球表面的重力加速度是地球表面的1/6).若要把此摆钟调准，应使摆长L₀调节为______________.

如图11-4-11所示是演示沙摆振动图象的实验装置，沙摆的运动可看作简谐运动.若用手向外拉木板的速度是0.20 m/s，木板的长度是0.60 m，那么这次实验所用的沙摆的摆长为__________ m.（答案保留两位有效数字，计算时可取π²=g）

图11-4-11

为了测量某一弹簧的劲度系数，将该弹簧竖直悬挂起来，在自由端挂上不同质量的砝码．实验测出了砝码质量m与弹簧长度l的相应数据，其对应点已在图上标出．(g＝9.8 m/s²)

(1)作出m－l的关系图线；
(2)弹簧的劲度系数为________N/m．