高中物理力学实验计算题

如右图所示，两个带等量异种电荷、竖直正对放置、电容为C、间距为d的平行金属板，两板间的电场可视为匀强电场．将一个质量为m、电荷量为－q的带电小球，用长度为L（L＜d）的、不可伸长的绝缘细线悬挂于两板间电场中的O点．此外在两板之间还存在着一种特殊物质（图中未画出），这种物质能使处于电场中的小球受到一个大小为F＝kv（k为常数，v为小球的速率）、总是背离圆心方向的力．现将小球拉至细线刚好伸直但不绷紧的位置M，某时刻由静止释放小球，当小球向下摆过60°到达N点时，小球的速度恰好为零．若在小球下摆过程中，细线始终未松弛，重力加速度取g，不考虑空气阻力的影响，试求：
⑴左侧金属板所带的电荷量Q是多少？
⑵小球到达N点时的加速度大小是多少？

某物理兴趣小组的同学在研究弹簧弹力的时候，测得弹力的大小
F和弹簧长度L的关系如图所示，则由图线可知：
（1）弹簧的劲度系数为                  。
（2）弹簧的弹力为5N，弹簧的长度为        。

如图所示，将一质量为m="0.1Kg" 的小球自水平平台右端O点以初速度v₀水平抛出，小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC，到达轨道最高点C时，小球的速度为10m/s，圆轨道ABC的形状为半径为R=2.5m的圆截去了左上角的127°的圆弧，CB为其竖直直径，sin37°=0.6，g=10m/s²，

小球运动到轨道最低点B时，轨道对小球的支持力多大？
平台末端O点到A点的竖直高度H

如图，一块质量为M = 2kg，长L = 1m的匀质木板放在足够长的光滑水平桌面上，初始时速度为零．板的最左端放置一个质量m = 1kg的小物块，小物块与木板间的动摩擦因数为μ = 0.2，小物块上连接一根足够长的水平轻质细绳，细绳跨过位于桌面边缘的定滑轮（细绳与滑轮间的摩擦不计，木板与滑轮之间距离足够长，g = 10m/s²）。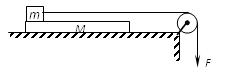

若木板被固定，某人以F= 4N向下拉绳，则小木块滑离木板所需要的时间是多少？
整个过程恒力F做多少功？
若木板不固定，某人仍以恒力F = 4N向下拉绳，则小木块滑离木板所需要的时间是多少？整个过程恒力F做多少功？

一只足球以8m/s的速度沿正东方向运动，运动员飞起一脚，足球以10m/s的速度向正西方向飞去，远动员与足球的作用时间为0.1s，求足球获得加速度的大小和方向．

表演“水流星”节目，如图所示,拴杯子的绳子长为，绳子能够承受的最大拉力是杯子和杯内水重力的8倍.要使绳子不断,节目获得成功,重力加速度为g,求：

杯子通过最高点时速度的最小值为多大？
通过最低点时速度的最大值为多大？

如图所示，一质量为M＝5.0kg的平板车静止在光滑水平地面上，平板车的上表面距离地面高h＝0.8m，其右侧足够远处有一固定障碍物A．另一质量为m＝2.0kg可视为质点的滑块，以v₀＝8m/s的水平初速度从左端滑上平板车，同时对平板车施加一水平向右、大小为5N的恒力F．当滑块运动到平板车的最右端时，两者恰好相对静止．此时车去恒力F．此后当平板车碰到障碍物A时立即停止运动，滑块水平飞离平板车后，恰能无碰撞地沿圆弧切线从B点切入光滑竖直圆弧轨道，并沿轨道下滑．已知滑块与平板车间的动摩擦因数μ＝0.5，圆弧半径为R＝1.0m，圆弧所对的圆心角∠BOD＝θ＝106⁰，g取10m/s²，sin53⁰＝0.8，cos53⁰＝0.6，不计空气阻力，求：

（1）平板车的长度；
（2）障碍物A与圆弧左端B的水平距离；
（3）滑块运动圆弧轨道最低点C时对轨道压力的大小．

如图所示，长为的细线一端固定在O点，另一端拴一质量为m的小球，现使小球恰好能在竖直平面内做完整的圆周运动，已知O点到水平地面的距离Soc =L且 L>，重力加速度为g

求小球通过最高点A时的速度v_A的大小．
求小球通过最低点B时，细线对小球的拉力．
求小球运动到A点或B点时细线断裂，小球落到地面对到C点的距离若相等，则和L应满足什么关系？

某游乐场的过山车从较高的弧形轨道顶部，从静止开始向下运动，在底部进入与之连接的圆形轨道，它可以底朝上在竖直圆轨道顶部运行，游客不会掉下来，如图（甲）所示，可以把这种情形抽象为如图（乙）所示的简图，为了游客的安全，载人过山车在通过圆轨道的最高点时，对轨道要有一定的压力，假设该压力为人与过山车总重力的0.5倍，圆轨道的半径为R，不考虑一切阻力，问：

弧形轨道顶部到底部的高度应多大？
若人的质量为，过山车经过圆轨道最低点时人对座椅的压力多大？

如图，一个质量为0．6kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）。已知圆弧的半径R=0．3m， θ="60" 0，小球到达A点时的速度 v="4" m/s 。（取g ="10" m/s2）求：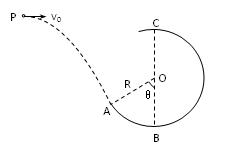
小球做平抛运动的初速度v0 ；
P点与A点的水平距离和竖直高度；
小球到达圆弧最高点C时对轨道的压力。

m为在水平传送带上被传送的小物体（可视为质点），A为终端皮带轮，如图所示，已知皮带轮半径为r，传送带与皮带轮间、传送带与小物体间不会打滑，当m可被水平抛出时，求：
A轮每秒的转数n最少是多少？
若A轮有上述的最小转速，且其最高点距地面高度为h，求小物体落地的速度方向（用反三角函数表示）．

环保汽车将为2008年奥运会场馆服务。某辆以蓄电池为驱动能源的环保汽车，总质量m＝3×10³ kg。当它在水平路面上以v＝36 km/h的速度匀速行驶时，驱动电机的输入电流I＝50 A，电压U＝300 V。在此行驶状态下。
求驱动电机的输入功率P_电；
若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P_机，求汽车所受阻力与车重的比值（g取10 m/s²）；
设想改用太阳能电池给该车供电，其他条件不变，求所需的太阳能电池板的最小面积。结合计算结果，简述你对该设想的思考。已知太阳辐射的总功率P₀＝4×10²⁶ W，太阳到地球的距离r＝1.5×10¹¹ m，太阳光传播到达地面的过程中大约有30%的能量损耗，该车所用太阳能电池的能量转化效率约为15%。

如图所示，A，B为两个大小可视为质点的小球，A的质量，B的质量，B球用长的轻质细绳吊起，当细绳位于竖直位置，B球处于静止状态时，B球恰好与弧形轨道MN的末端接触但无作用力，已知弧形轨道的内表面光滑，且末端切线水平，现使A球从距轨道末端的高处由静止释放，当A球运动到轨道末端时与B球发生完全弹性碰撞。若取，求：
A球刚要接触到B球时的速度大小；
两小球相碰撞过程中，B球对A球所做的功；
两个小球碰撞后各自开始运动的瞬间，B球对细绳的拉力大小。

一位质量为的运动员用的时间跑完路程。设他从开始起跑的前4.0s时间作的是匀加速直线运动，后8.0s时间则作匀速直线运动，速度大小等于第4.0s末时的瞬时速度。已知他在整个运动过程中受到的阻力保持不变，大小为72N。求
他在跑这100m过程中做功的平均功率；
他的瞬时功率的最大值。

如图所示，一物体从光滑斜面顶端由静止开始下滑。已知物体的质量，斜面的倾角，斜面长度，重力加速度取。求：

物体滑到斜面底端时重力对物体做功的瞬时功率。
物体下滑的全过程中重力做功的平均功率。
物体下滑的全过程中斜面的支持力对物体的冲量大小。