做简谐运动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减
小为原来的1/2,则单摆振动的
| A.频率、振幅都不变 | B.频率、振幅都改变 |
| C.频率不变、振幅改变 | D.频率改变、振幅不变 |
竖直上抛运动的物体,在它到达最高点时:
| A.速度为零,加速度也为零 |
| B.速度为零,但加速度不为零,方向竖直向下 |
| C.速度为零,但加速度不为零,方向竖直向上 |
| D.具有竖直向下的速度和竖直向下的加速度 |
关于运动的性质,以下说法中正确的是( )
| A.曲线运动一定是变速运动 |
| B.变速运动一定是曲线运动 |
| C.曲线运动一定是变加速运动 |
| D.运动物体的加速度大小、速度大小都不变的运动一定是直线运动 |
2、如果两个不在同一直线上的分运动都是初速度为零的匀加速度直线运动,则( )
| A.合运动是直线运动 |
| B.合运动是曲线运动 |
| C.合运动可能是直线运动,也可能是曲线运动 |
| D.只有当两个分运动的加速度大小相等时,合运动才是直线运动 |
如图8-8-3所示,质量为0.5 kg的小球在距离车底面高20 m处以一定的初速度向左平抛,落在以7.5 m/s速度沿光滑水平面向右匀速行驶的敞篷小车中,车底涂有一层油泥,车与油泥的总质量为4 kg.设小球在落到车底前瞬间速度是25 m/s,则当小球与小车相对静止时,小车的速度是( )

图8-8-3
| A.5 m/s | B.4 m/s | C.8.5 m/s | D.9.5 m/s |
质量为  的小球以
的小球以  的速度与质量为
的速度与质量为  的静止小球正碰,关于碰后的速度,下面哪些是可能的( )
的静止小球正碰,关于碰后的速度,下面哪些是可能的( )
A. |
B. |
C. |
D. |
窗体顶端
有一秒摆T="2" s,摆球的质量为0.04 kg,当摆球质量增加到0.08 kg时,它的周期是_______,当摆长增加到原来的4倍时,它的振动频率是_________。
用单摆测重力加速度的实验中,若测得的重力加速度g值偏大,其原因可能是下列中的( )
| A.振幅太小,测得的周期偏小 |
| B.计算摆长时,只考虑线长,没有加上摆球半径 |
| C.将n次全振动误记为(n-1)次全振动 |
| D.将n次全振动误记为(n+1)次全振动 |
一个单摆由甲地移到乙地后,发现走时变快了,其变快的原因及调整的方法是( )
| A.g甲>g乙,将摆长缩短 | B.g甲<g乙,将摆长放长 |
| C.g甲<g乙,将摆长缩短 | D.g甲>g乙,将摆长放长 |
一根摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s.
(1)求当地的重力加速度g;
(2)该单摆拿到月球上去,已知月球的重力加速度是1.60 m/s2,单摆振动周期是多少?
下面是用单摆测定重力加速度实验中获得的有关数据:
| 摆长l/m |
0.5 |
0.6 |
0.8 |
1.1 |
| 周期T2/s2 |
2.2 |
2.5 |
3.2 |
4.5 |
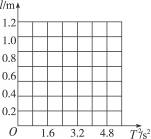
图11-4
(1)利用上述数据在坐标图中描出l-T2图象.
(2)利用图象,取T2=0.1×4π2s2=3.95s2,求重力加速度.
一个秒摆摆球的质量为0.2 kg,它振动到最大位移时距最低点的高度为0.4 cm,它完成10次全振动回到最大位移时,距最低点的高度变为0.3 cm,如果每完成10次全振动给它补充一次能量,使摆球回到原来的高度,在60 s内总共补充的能量是____________________.
利用高楼楼顶下垂的单摆、实验室用的刻度尺和秒表,如何测定当地的重力加速度?请你设计一种行之有效的方法,写出简要的实验原理及计算g值的公式.(注意:单摆摆长无法直接测出)
为了使单摆做简谐运动的周期变长,可以使( )
| A.单摆的振幅适当加大 | B.单摆的摆长适当加长 |
| C.单摆从山下移到山上 | D.单摆从北京移到南极 |