(1)一静止的铝原子核 俘获一速度为 的质子p后,变为处于激发态的硅原子核 ,下列说法正确的是_________
| A. | 核反应方程为 |
| B. | 核反应方程过程中系统动量守恒 |
| C. | 核反应过程中系统能量不守恒 |
| D. | 核反应前后核子数相等,所以生成物的质量等于反应物的质量之和 |
| E. | 硅原子核速度的数量级为 ,方向与质子初速度方向一致 |
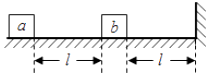
(2)如图所示,水平地面上有两个静止的小物块a和b,其连线与墙垂直:a和b相距l;b与墙之间也相距l;a的质量为m,b的质量为 ,两物块与地面间的动摩擦因数均相同,现使a以初速度 向右滑动,此后a与b发生弹性碰撞,但b没有与墙发生碰撞,重力加速度大小为g,求物块与地面间的动摩擦力因数满足的条件。
中子的质量为1.008 7 u,质子的质量为1.007 3 u,氘核的质量为2.013 6 u,求中子和质子结合成氘核时释放的能量.
一个氢原子的质量为1.6736×10-27kg,一个锂原子的质量为11.6505×10-27kg,一个氦原子的质量为6.6467×10-27kg。一个锂核受到一个质子轰击变为2个α粒子,⑴写出核反应方程,并计算该反应释放的核能是多少?⑵1mg锂原子发生这样的反应共释放多少核能?
为确定爱因斯坦的质能方程 的正确性,设计了如下实验:用动能为
的正确性,设计了如下实验:用动能为 0MeV的质子轰击静止的锂核
0MeV的质子轰击静止的锂核 ,生成两个
,生成两个 粒子,测得两个
粒子,测得两个 粒子的动能之和为
粒子的动能之和为 MeV,已知质子、
MeV,已知质子、 粒子、锂粒子的质量分别取
粒子、锂粒子的质量分别取 、
、 、
、 ,求:
,求:
(1)写出该反应方程。
(2)通过计算说明 正确。(1u = 1.6606×10-27㎏)
正确。(1u = 1.6606×10-27㎏)
中子 、质子
、质子 、氘核D的质量分别为mn、mp、mD.现用光子能量为E的γ射线照射静止氘核,使之分解.用核符号写出上述核反应方程,若分解后的中子、质子的动能相等,则中子的动能是多少?
、氘核D的质量分别为mn、mp、mD.现用光子能量为E的γ射线照射静止氘核,使之分解.用核符号写出上述核反应方程,若分解后的中子、质子的动能相等,则中子的动能是多少?
已知氘核质量为2.013 6 u,中子质量为1.008 7 u, 的质量为3.015 0 u.
的质量为3.015 0 u.
(1)写出两个氘核聚变成 的核反应方程;
的核反应方程;
(2)计算上述核反应中释放的核能;
(3)若两氘核以相等的动能0.35 MeV做对心碰撞即可发生上述核反应,且释放的核能
全部转化为机械能,则反应中生成的 和中子的动能各是多少?
和中子的动能各是多少?
思路点拨:(1)计算出质量亏损Δm,根据ΔE=Δmc2计算释放的核能.(2)在两氘核对心碰撞发生核反应的过程中,满足动量守恒及能的转化与守恒定律.
太阳内部持续不断地发生着4个质子聚变为1个氦核的热核反应,这个核反应释放出的大量能量就是太阳的能源.
(1)写出这个核反应方程;
(2)这一核反应能释放多少能量?
(3)已知太阳每秒释放的能量为3.8×1026 J,则太阳每秒减少的质量为多少?
(4)若太阳质量减少万分之三,热核反应不能继续进行,计算太阳能存在多少年.(太阳质量M=2×1030 kg,mp=1.007 3 u,mHe=4.001 5 u,me=0.000 55 u)