为确定爱因斯坦的质能方程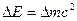
的正确性，设计了如下实验：用动能为
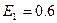0MeV的质子轰击静止的锂核
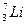，生成两个
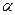粒子，测得两个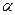粒子的动能之和为
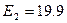MeV，已知质子、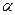粒子、锂粒子的质量分别取
、
、
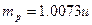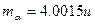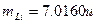，求：
（1）写出该反应方程。
（2）通过计算说明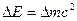正确。（1u = 1.6606×10-27㎏）
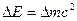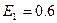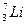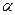为确定爱因斯坦的质能方程的正确性，设计了如下实验：用动能为0MeV的质子轰击静止的锂核，生成两个粒子，测得两个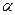粒子的动能之和为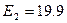MeV，已知质子、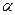粒子、锂粒子的质量分别取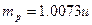、、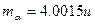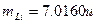，求：
（1）写出该反应方程。
（2）通过计算说明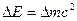正确。（1u = 1.6606×10-27㎏）
，请画出受力分析图并求绳ON和绳OM受到的拉力的大小？
粤公网安备 44130202000953号