高中物理放射性同位素的应用计算题

如图所示，半径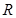=0.4m的光滑半圆环轨道处于竖直平面内，半圆环与粗糙的水平地面相切于圆环的端点A．一质量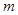=0.1kg的小球，以初速度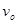=8m/s在水平地面上向左作加速度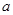=4m/s²的匀减速直线运动，运动4m后，冲上竖直半圆环，经过最高点B最后小球落在C点。取重力加速度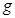=10m/s²。求：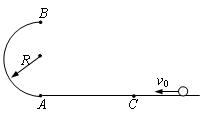

（1）小球到达A点时速度大小；
（2）小球经过B点时对轨道的压力大小；
（3）A、C两点间的距离。

一辆值勤的警车停在公路边，当警员发现从他旁边以v＝8 m/s的速度匀速行驶的货车有违章行为时，决定前去追赶，经2.5 s，警车静止开始发动起来，以加速度a＝2 m/s²做匀加速运动，试问：
(1)警车要经多长时间才能追上违章的货车？
(2)在警车追上货车之前，两车间的最大距离是多少？

有时飞机需要在航空母舰的甲板上起飞，将飞机起飞的运动简化为匀加速直线运动。已知某型号的战斗机的发动机起飞时能产生的最大加速度为4.5 m/s²，，所需的起飞速度为60m/s，请分析：
（1）若飞机仅依靠自身的发动机起飞，飞机需要的跑道至少应多长？
（2）若航空母舰的跑道长300m，那么帮助飞机起飞的弹射系统应使飞机至少具有多大的初速度？

一列汽车车队以v₁=10m/s的速度匀速行驶，相邻车间距为25m，后面有一辆摩托车以v₂=20m/s的速度同向行驶，当它与车队最后一辆车相距S₀=40m时刹车，以=0.5m/s²的加速度做匀减速直线运动，摩托车从车队旁边行驶而过，设车队车辆数n足够多，问：
（1）摩托车最多与几辆汽车相遇？摩托车与车队中汽车共相遇几次？
（2）摩托车从赶上车队到离开车队，共经历多少时间？(结果可用根号表示)

如图所示，一质量为M的楔形木块放在水平桌面上，它的顶角为90°，两底角为α和β；a、b为两个位于斜面上质量均为m的小木块。已知所有接触面都是光滑的。现使a、b同时沿斜面下滑。（1）通过计算解释为什么楔形木块静止不动（2）求楔形木块对水平桌面的压力。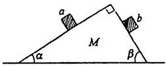

如图，长为L=2m、质量m_A＝4kg的木板A放在光滑水平面上，质量m_B＝1kg的小物块（可视为质点）位于A的中点，水平力F作用于A.AB间的动摩擦因素μ=0.2(AB间最大静摩擦力等于滑动摩擦力，g=10m/s²)。求：

(1)为使AB保持相对静止，F不能超过多大？
(2)若拉力F＝12N，物块B从A板左端滑落时木板A的速度为多大？

(16分)驾驶证考试中的路考，在即将结束时要进行目标停车，考官会在离停车点不远的地方发出指令，要求将车停在指定的标志杆附近，终点附近的道路是平直的，依次有编号为A、B、C、D、E的五根标志杆，相邻杆之间的距离△L=16.0m。一次路考中，学员甲驾驶汽车，学员乙坐在后排观察并记录时间，学员乙与车前端面的距离为△s=2.0m。假设在考官发出目标停车的指令前，汽车是匀速运动的，当学员乙经过O点考官发出指令：“在D标志杆目标停车”，发出指令后，学员乙立即开始计时，学员甲需要经历 △t=0.5s的反应时间才开始刹车，开始刹车后汽车做匀减速直线运动，直到停止。学员乙记录下自己经过B、C杆时的时刻t_B=5.50s，t_C=7.50s。已知O、A间的距离L_OA=69m。求：

（1）刹车前汽车做匀速运动的速度大小v₀及汽车开始刹车后做匀减速直线运动的加速度大小a；
（2）汽车停止运动时车头前端面离D的距离。

如图（1）所示，一根直杆AB与水平面成某一角度自定，在杆上套一个小物块，杆底端B处有一弹性挡板，杆与板面垂直，现将物块拉到A点由静止释放，物块下滑与挡板第一次碰撞前后的v－t图像如图（2）所示，物块最终停止在B点．重力加速度为g＝10m／s²，求：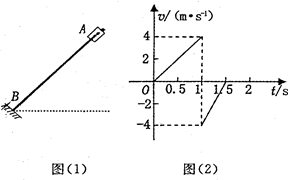

（1）物块与杆之间的动摩擦因数μ；
（2）物块滑过的总路程s．

2014年12月26日，我国东部14省市ETC联网正式启动运行，ETC是电子不停车收费系统的简称。汽车分别通过ETC通道和人工收费通道的流程如图所示。假设汽车以v₁=15m／s朝收费站正常沿直线行驶，如果过ETC通道，需要在收费站中心线前l0 m处正好匀减速至v₂="5" m／s，匀速通过中心线后，再匀加速至v₁正常行驶；如果过人工收费通道，需要恰好在中心线处匀减速至零，经过20 s缴费成功后，再启动汽车匀加速至v₁正常行驶。设汽车加速和减速过程中的加速度大小均为l m／s²。求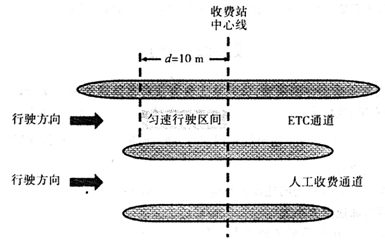

（1）汽车过ETC通道时，从开始减速到恢复正常行驶过程中的位移大小
（2）汽车通过ETC通道比通过人工收费通道节约的时间是多少

如图所示，绷紧的水平传送带足够长，且始终以v₁=2m/s的恒定速率运行。初速度大小为v₂="3" m/s的小墨块从与传送带等高的光滑水平地面上的A处滑上传送带。若从小墨块滑上传送带开始计时，小墨块在传送带上运动5s后与传送带的速度相同，求小墨块在传送带上留下的痕迹。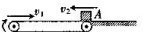

摩托车从A点由静止出发做匀加速直线运动,用7s时间通过一座长BC=14m的平桥,过桥后的速度是3m/s。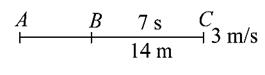

(1)它刚开上桥头时的速度v_B有多大?
(2)桥头与出发点相距多远?

如图，将质量m=2kg的圆环套在与水平面成角的足够长直杆上，直杆固定不动，环的直径略大于杆的截面直径，杆上依次有三点A、B、C，s_AB=8m，s_BC=0.6m，环与杆间动摩擦因数，对环施加一个与杆成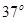斜向上的拉力F，使环从A点由静止开始沿杆向上运动。已知t=4s时环到达B点．重力加速度g=10m／s²，。

（1）求F的大小；
（2）若到达B点时撤去力F，求此环到达C点所用的时间．

如图甲所示是一打桩机的简易模型。质量m=1kg的物体在拉力F作用下从与钉子接触处由静止开始运动，上升一段高度后撤去F，到最高点后自由下落，撞击钉子，将钉子打入一定深度。物体上升过程中，机械能E与上升高度h的关系图象如图乙所示。不计所有摩擦，g取10m/s²。求：

（1）物体上升1 m后再经多长时间才撞击钉子（结果可保留根号）；
（2）物体上升到0.25m高度处拉力F的瞬时功率。

“30m折返跑”中．在平直的跑道上，一学生站立在起点线处，当听到起跑口令后（测试员同时开始计时），跑向正前方30m处的折返线，到达折返线处时，用手触摸固定的折返处的标杆，再转身跑回起点线，到达起点线处时，停止计时，全过程所用时间即为折返跑的成绩．学生可视为质点，加速或减速过程均视为匀变速，触摸杆的时间不计．该学生加速时的加速度大小为a₁=2.5m/s²，减速时的加速度大小为a₂=5m/s²，到达折返线处时速度需减小到零，并且该学生全过程最大速度不超过V_m=12m/s．求该学生“30m折返跑”的最好成绩．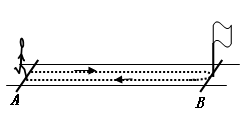

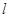冰壶在水平而上某次滑行可简化为如下过程：如图所示，运动员给冰壶施加一水平恒力将静止于A点的冰壶（视为质点）沿直线AD推到B点放手，最后冰壶停于D点。已知冰壶与冰面间的动摩擦因数为，AB=CD=、BC=7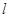，重力加速度为g。求：

(1)冰壶经过B点时的速率；
(2)冰壶在CD段与在AB段运动的时间之比。