高中物理放射性同位素的应用计算题

甲、乙两个同学在直跑道上进行4×100 m接力（如图所示），他们在奔跑时有相同的最大速度，乙从静止开始全力奔跑需跑出25 m才能达到最大速度，这一过程可看作匀加速直线运动．现在甲持棒以最大速度向乙奔来，乙在接力区伺机全力奔出．若要求乙接棒时奔跑的速度达到最大速度的80%，则：

（1）乙在接力区须奔出多少距离？
（2）乙应在距离甲多远时起跑？

质量M＝0.2 kg的小圆环穿在固定的足够长的斜木杆上，斜木杆与水平方向的夹角θ＝37°，小圆环与木杆间的动摩擦因数μ＝0.5，小圆环受到竖直向上的恒定拉力F＝3 N后，由静止开始沿木杆斜向上做匀加速直线运动（sin37°＝0.6，cos37°＝0.8，g取10 m/s²），求：

（1）小圆环沿斜木杆向上的合外力为多少；
（2）4 s末小圆环的速度为多少？

如图甲所示，一质量为m=1kg的物块静止在粗糙水平面上的A点，从t=0时刻开始，物体在受按如图乙所示规律变化的水平力F作用下向右运动，第3s末物块运动到B点时速度刚好为0，第5s末物块刚好回到A点，已知物块与粗糙水平间的动摩擦因数μ=0.2（g取10m/s²），求：

（1）AB间的距离；
（2）水平力F在5s时间内对物块的冲量。

如图，足够长的斜面倾角θ=37°。一个物体以v₀=12m/s的初速度从斜面A点处沿斜面向上运动。物体与斜面间的动摩擦因数为μ=0．25。已知重力加速度g=10m/s²，sin37°=0．6，cos37°=0．8。求：

（1）物体沿斜面上滑时的加速度大小a₁；
（2）物体沿斜面上滑的最大距离x；
（3）物体沿斜面到达最高点后返回下滑时的加速度大小a₂；
（4）物体从A点出发到再次回到A点运动的总时间t。

质量的带电荷量的小球从某一点静止释放，运动秒后空间出现竖直方向的匀强电场，再经过秒，小球又回到出发点，不计空气阻力且始终没有落地。求电场强度E。

如图所示，将小物体（可视为质点）置于桌面上的薄纸板上，用水平向右的恒力F拉动纸板，拉力大小不同，纸板和小物体的运动情况也不同。若纸板的质量m₁=0.1kg，小物体的质量m₂=0.4kg，小物体与桌面右边缘的距离d=0.15m，已知各接触面间的动摩擦因数均为μ=0.2，最大静摩擦力与滑动摩擦力相等，g取10m/s²。求：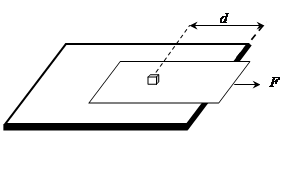

（1）当小物体与纸板一起运动时，桌面给纸板的摩擦力大小；
（2）拉力F满足什么条件，小物体才能与纸板发生相对滑动；
（3）若拉力作用0.3s时，纸板刚好从小物体下抽出，通过计算判断小物体是否会留在桌面上。m]

如图所示，一传送皮带与水平面夹角为=37°，正以2 m/s的恒定速率顺时针运行。现将一质量为10kg的工件轻放于其底端，经一段时间送到高3 m的平台上，已知工件与皮带间的动摩擦因数为μ=，g取10 m/s²，求带动皮带的电动机由于传送工件多消耗的电能。

如图所示，水平传送带的速度为4.0m/s，它的右端与等高的光滑水平平台相接触。一工件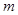（可看成质点）轻轻放在传送带的左端，工件与传送带间的动摩擦因数μ=0.3，经过一段时间工件从光滑水平平台上滑出，恰好落在小车左端，已知平台与小车的高度差h=0.8，小车左端距平台右端的水平距离为s=1.2m，取g=10m/s²，求：

（1）工件水平抛出的初速度v₀是多少？
（2）传送带的长度L是多少？

质量为2×10³ kg的汽车，发动机输出功率为30×10³ W．在水平公路上能达到的最大速度为15 m/s，设阻力恒定。求：
（1）汽车所受的阻力f
（2）汽车的速度为10m/s时，加速度a的大小
（3）若汽车从静止开始保持2m/s²的加速度作匀加速直线运动，则这一过程能持续多长时间？

如图所示，传送带长6 m，与水平方向的夹角，以5 m/s的恒定速度向上运动。一个质量为2 kg的物块（可视为质点），沿平行于传送带方向以10 m/s的速度滑上传送带，已知物块与传送带之间的动摩擦因数μ=0．5，sin37°=0．6，cos37°=0．8，g=10m/s²。
求：

（1）物块刚滑上传送带时的加速度大小；
（2）物块到达传送带顶端时的速度大小；
（3）整个过程中，摩擦力对物块所做的功。

如图，在倾角为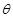=37°的足够长固定斜面底端，一质量m=1kg的小物块以某一初速度沿斜面上滑，一段时间后返回出发点。物块上滑所用时间t₁和下滑所用时间t₂大小之比为t₁：t₂=1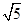：取g=10m／s²，sin37°=0.6，cos37°=0.8。求：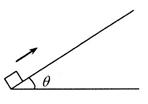

（1）物块由斜面底端上滑时的初速度v₁与下滑到底端时的速度v₂的大小之比；
（2）物块和斜面之间的动摩擦因数；
（3）若给物块施加一大小为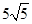N、方向与斜面成适当角度的力，使物块沿斜面向上加速运动，求加速度的最大值。

如图所示，生产车间有两个相互垂直且等高的水平传送带甲和乙，甲的速度为v₀。质量均为m的工件离开甲前与甲的速度相同，并平稳地传到乙上，工件与乙之间的动摩擦因数为μ。乙的宽度足够大，重力加速度为g。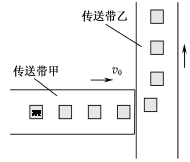

（1）若乙保持静止，求某工件在乙上滑行的距离；
（2）若乙的速度也为v₀，求：
①刚滑上乙时，某工件受到摩擦力的大小和方向；
②某工件在乙上垂直于传送带乙的运动方向滑行的距离；
③某工件在乙上滑行的过程中产生的热量。
（3）若乙的速度为v，试判断某工件在乙上滑行的过程中所受摩擦力是否发生变化，并通过分析和计算说明理由。

低空跳伞是一种极限运动，一般在高楼、悬崖、高塔等固定物上起跳。人在空中降落过程中所受空气阻力随下落速度的增大而增大，而且速度越大空气阻力增大得越快。因低空跳伞下落的高度有限，导致在空中调整姿态、打开伞包的时间较短，所以其危险性比高空跳伞还要高。
一名质量为70kg的跳伞运动员背有质量为10kg的伞包从某高层建筑顶层跳下，且一直沿竖直方向下落，其整个运动过程的v－t图象如图所示。已知2.0s末的速度为18m/s，10s末拉开绳索开启降落伞，16.2s时安全落地，并稳稳地站立在地面上。g取10m/s²，请根据此图象估算：

（1）起跳后2s内运动员（包括其随身携带的全部装备）所受平均阻力的大小；
（2）运动员从脚触地到最后速度减为零的过程中，若不计伞的质量及此过程中的空气阻力，则运动员所需承受地面的平均冲击力多大；
（3）开伞前空气阻力对跳伞运动员（包括其随身携带的全部装备）所做的功（结果保留三位有效数字）。

如图甲所示，倾角θ =37°的粗糙斜面固定在水平面上，斜面足够长。一根轻弹簧一端固定在斜面的底端，另一端与质量m=1.0kg的小滑块（可视为质点）接触，滑块与弹簧不相连，弹簧处于压缩状态。当t=0时释放滑块。在0~0.24s时间内，滑块的加速度a随时间t变化的关系如图乙所示。已知弹簧的劲度系数N/m，当t=0.14s时，滑块的速度v₁=2.0m/s。g取l0m/s²，sin37°=0.6，cos37°=0.8。弹簧弹性势能的表达式为（式中k为弹簧的劲度系数，x为弹簧的形变量）。求：

图甲                                图乙
（1）斜面对滑块摩擦力的大小f；
（2）t=0.14s时滑块与出发点间的距离d；
（3）在0~0.44s时间内，摩擦力做的功W。

拥堵已成为现代都市一大通病，发展“空中轨道列车”（简称空轨）是缓解交通压力重要举措。如图所示，它是一种悬挂式单轨交通系统，不仅施工简单、快捷，造价也仅为地铁造价的六分之一左右，下表是有关空轨列车的部分参数。假如多辆空轨列车在同一轨道上同向行驶，为了安全，前后车之间应保持必要的距离，假设前方车辆突然停止，后车司机从发现这一情况，经操纵刹车，到汽车开始减速所经历的时间（即反应时间）t=0.50s，求空轨列车的安全车距应至少设定为多少？（g=10m/s²）

行车速度	约13 m/s	车辆起动加速度	1.0 m/s^2
车辆高度	2623 mm	紧急制动加速度	6.50 m/s^2
车辆宽度	2244 mm	车辆净重	8455 kg
平面转弯半径	≥30 m	车辆满载重	15000kg