8两个相同的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两小球,然后,用一水平方向的力F作用在小球A上,此时三根细线均处于直线状态,且OB细线恰好处于竖直方向,如图所示。如果不考虑小球的大小,两小球均处于静止状态,则
(1)OB绳对小球的拉力为多大?
(2)OA绳对小球的拉力为多大?
(3)作用力F为多大?
如图所示,物体的质量为2kg,两根轻绳AB和AC的一端连接于竖直墙上,另一端系于物体上,在物体上另施加一个方向与水平线成θ=600的拉力F,若要使两绳都能伸直,求拉力F的大小范围。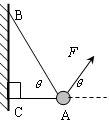
人类的陆上运输经历了从马车到蒸汽机车,再到内燃机车的演变过程。今天,我们已拥有汽车、火车、飞机等快速变通工具。
| 1. |
汽车、火车、飞机在行驶中都会因某些因素而影响其速度,所以高速运行的交通工具的头部一般呈流线型,主要是为了减少。 |
| 2. |
某汽车的部分参数如下表,请根据表中数据完成表的其他部分。
|
| 3. |
生活中经常用"呼啸而来"形容正在驶近的车辆,这是声波在传播过程中对接收者而言频率发生变化的表现,无线电波也具有这种效应。图中的测速雷达正在向一辆接近的车辆发生无线电波,并接收被车辆反射的无线电波。由于车辆的运动,接收的无线电波频率与发生时不同,利用频率差 |
| 4. |
有一个小实验:当向两片竖直放置的纸片的中间吹气时,会发现两个小纸片不但不分离,反而靠拢了。这一现象告诉我们,流体运动部分产生的压强要比它周围静止部分产生的压强小。也可以概括为流速大,压强小、流速小,压强大。飞机上天就是由于机翼上下空气流速不同造成的压力差所致。
|
| 5. |
电动车所需能量由它所携带的蓄电池供给。右图为某类电动车与汽油车性能的比较。通常车用电动机的质量是汽油机的4倍或5倍。为促进电动车的推广使用,在技相主主要应对电动车的等部件加以改进。给电动车蓄电池充电的能量实际上来自于发电站。一般发电站燃烧燃料所释放出来的能量仅30%转化为电能,在向用户输送及充电过程中又损失了20%,这意味着使用电动车时能量转化的总数率约为%。
|
我国北方地区近年来遭遇严重的沙尘暴天气,现把沙尘上扬后的情况简化为如下情景:v为竖直向上的风速,沙尘颗粒被扬起后悬浮在空中(不动),这时风对沙尘的作用力相当于空气不动而沙尘以速度 v竖直向下运动时所受的阻力。此阻力可用下式表达 其中
其中 为一系数,A为沙尘颗粒的截面积,
为一系数,A为沙尘颗粒的截面积, 为空气密度。(球体体积
为空气密度。(球体体积 )
)
(1)若沙粒的密度 ,沙尘颗粒为球形,半径为r,地球表面处空气密度
,沙尘颗粒为球形,半径为r,地球表面处空气密度 ,试估算在地面附近上述v的最小值。
,试估算在地面附近上述v的最小值。
(2)假定空气密度 随高度h的变化关系为
随高度h的变化关系为 其中
其中 为h
为h 处的空气密度,C为一常量,试估算当
处的空气密度,C为一常量,试估算当 、扬沙稳定时的最大高度。(不考虑g随高度的变化)
、扬沙稳定时的最大高度。(不考虑g随高度的变化)
当物体从高空下落时,所受阻力会随物体的速度增大而增大,因此经过下落一段距离后将匀速下落,这个速度称为此物体下落的收尾速度。研究发现,在相同环境条件下,球形物体的收尾速度仅与球的半径和质量有关.下表是某次研究的实验数据
| 小球编号 |
A |
B |
C |
D |
E |
| 小球的半径(×10-3m) |
0.5 |
0.5 |
1.5 |
2 |
2.5 |
| 小球的质量(×10-6kg) |
2 |
5 |
45 |
40 |
100 |
| 小球的收尾速度(m/s) |
16 |
40 |
40 |
20 |
32 |
(1)根据表中的数据,求出B球与C球在达到终极速度时所受阻力之比.
(2)根据表中的数据,归纳出球型物体所受阻力f与球的速度大小及球的半径的关系(写出有关表达式、并求出比例系数).
(3)现将C号和D号小球用轻质细线连接,若它们在下落时所受阻力与单独下落时的规律相同.让它们同时从足够高的同一高度下落,试求出它们的收尾速度;并判断它们落地的顺序(不需要写出判断理由).
如图12所示粗细均匀的木棒长为L,质量为M ,可绕固定转动轴O自由转动,现用水平力F作用于木棒的下端将木棒从竖直位置缓慢拉起,并转过θ角度,则在拉起的过程中,拉力F做的功为多少?
某同学解法为:
木棒与竖直位置成θ时,木棒所受的力矩平衡 Mg Lsinθ/2=" F" Lcosθ,
得到F=Mgtgθ/2
从竖直位置缓慢拉起的过程中, 拉力F从0变化到Mgtgθ/2,
拉力F的平均值 =Mgtgθ/4
=Mgtgθ/4
拉力作用点在力F方向上的位移是 S="L" sinθ
根据W="FS " 解得 :拉力F 做的功:WF=" Mg" L sinθtgθ/4
所以在拉起的过程中,拉力F做的功为WF="Mg" L sinθtgθ/4 ,
你认为他的解法是否正确?若正确,请说明理由;若错误,也请说明理由,并且解出正确的结果。
如图1-71(原图1-69)所示,重为G的一根均匀硬棒AB,杆的A端被细绳吊起,在杆的另一端B作用一水平力F,把杆拉向右边,整个系统平衡后,细线、棒与竖直方向的夹角分别为a、b.求证:tgb=2tga.[15 ]
如图1-59(原图1-62)所示,重为600N的均匀木板搁在相距为2.0m的两堵竖直墙之间,一个重为800N的人站在离左墙0.5m处,求左、右两堵墙对木板的支持力大小.[7 ]
如图1-58(原图1-61)所示,一个质量为m、半径为R的球,用长为R的绳悬挂在L形的直角支架上,支架的重力不计,AB长为2R,BC长为 ,为使支架不会在水平桌面上绕B点翻倒,应在A端至少加多大的力?[6 ]
,为使支架不会在水平桌面上绕B点翻倒,应在A端至少加多大的力?[6 ]
如图所示,用两段直径均为d=0.02m,且相互平行的小圆棒A和B水平地支起一根长为L=0.64m、质量均匀分布的木条.设木条与两圆棒之间的静摩擦因数μ0=0.4,动摩擦因数μ=0.2.现使A棒固定不动.并对B棒施以适当外力,使木棒B向左缓慢移动,试讨论分析木条的移动情况,并把它的运动情况表示出来.设木条与圆棒B之间最先开始滑动.
如图所示,在xoy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与负x轴成45°角.在x<0且OM的左侧空间存在着负x方向的匀强电场E,场强大小为0.32N/C;在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场B,磁感应强度大小为0.1T.一不计重力的带负电的微粒,从坐标原点O沿y轴负方向以v0=2×103m/s的初速度进入磁场,最终离开电磁场区域.已知微粒的电荷量q=5×10-18C,质量m=1×10-24kg,求:
(1)带电微粒第一次经过磁场边界的位置坐标;
(2)带电微粒在磁场区域运动的总时间;
(3)带电微粒最终离开电、磁场区域的位置坐标.
如图所示,一轻质弹簧的一端固定于倾角为θ=300的光滑斜面上端,另一端系质量m=0.5kg的小球,小球被一垂直于斜面的挡板挡住,此时弹簧恰好为自然长度.现使挡板以恒定加速度a=2m/s2沿斜面向下匀加速运动(斜面足够长),己知弹簧的劲度系数k=50N/m.求:
(1)小球开始运动时挡板对小球提供的弹力.
(2)小球从开始运动到与挡板分离时弹簧的伸长量.
(3)试问小球与挡板分离后能否回到出发点?请简述理由.