在一次测试中,质量为1.6×103kg的汽车沿平直公路行驶,其发动机的输出功率恒为100kW。汽车的速度由10m/s增加到16m/s,用时1.7s,行驶距离22.6m。若在这个过程中汽车所受的阻力恒定,则汽车的速度为10m/s时牵引力的大小为 N,此时汽车加速度的大小为 m/s2。

如图,一绳绕过两个滑轮,一端系着质量为M的重物,另一端系着质量为m的浮于水上的小船,开始时小船静止,并设法使重物也静止.释放重物后,重物下降一段距离到达p处时,小船的速度为υ,此时系在船上的斜绳与水平方向所夹的锐角为θ.若不计滑轮、绳的质量及一切阻力,求上述过程中重力对质量为M的重物做的功。
把打桩机的重锤从离桩顶端2.0m高处自由下落,打到桩上,锤与桩的作用时间极短,作用后锤不弹起而与桩一起运动,桩被打入土中20cm深停止。如果桩受到地面的阻力大小跟它进入土中的深度成正比,并且桩受到土的阻力比桩和锤的重力要大得多。那么再把重锤升到原高度自由落下,这次打击能把桩再打入土中多深?
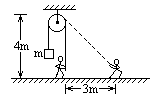
如图,一根绳子绕过高4m的滑轮(大小、摩擦均不计),绳的一端拴一质量为10kg的物体,另一侧沿竖直方向的绳被人拉住.若人拉住绳子前进3m,使物体匀速上升,则人拉绳所做的功为多大?
如图所示,一个静止的尖劈质量为M,被一个水平飞行的质量为m的小球击中,碰撞过程中没有动能损失,球相对地面竖直向上弹起,若尖劈碰撞后的速度为V,摩擦和空气阻力可忽略.求小球弹起的高度.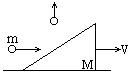
如图所示,A物体用板托着,位于离地h=1.0m处,轻质细绳通过光滑定滑轮与A、B相连,绳子处于绷直状态,已知A物体质量M=1.5㎏,B物体质量m=1.0kg,现将板抽走,A将拉动B上升,设A与地面碰后不反弹,B上升过程中不会碰到定滑轮,问:B物体在上升过程中离地的最大高度为多大?取g =10m/s2.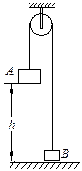
(1)从开始到木块刚好完全没入水的过程中,外力所做的功。
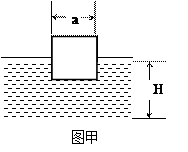
(2)若将该木块放在底面为正方形(边长为 a)的盛水足够深的长方体容器中,开始时,木块静止,有一半没入水中,如图乙所示,现用外力将木块缓慢竖直向下压,且始终没有水溢出,不计摩擦。求从开始到木块刚好完全没入水的过程中,容器中水的重力势能的改变量。
a)的盛水足够深的长方体容器中,开始时,木块静止,有一半没入水中,如图乙所示,现用外力将木块缓慢竖直向下压,且始终没有水溢出,不计摩擦。求从开始到木块刚好完全没入水的过程中,容器中水的重力势能的改变量。

如图20所示,光滑水平面AB与一半圆开轨道在B点相连,轨道位于竖直面内,其半径为R,一个质量为m的物块静止在水平面上,现向左推物块使其压紧弹簧,然后放手,物块在弹力作用下获得一速度,当它经B点进入半圆轨道瞬间,对轨道的压力为其重力的7倍,之后向上运动恰能完成半圆周运动到达C点,重力加速度为g。求:
(1)开始时弹簧所具有的弹性势能;
(2)物块从B到C克服阻力的功
(3)物块离开C点后,再落回到水平面上时速度的大小?
如图所示,质量是M的木板静止在光滑水平面上,木板长为l0,一个质量为m的小滑块以初速度v0从左端滑上木板,由于滑块与木板间摩擦作用,木板也开始向右滑动,滑块滑到木板右端时二者恰好相对静止,求:
(1)二者相对静止时共同速度为多少?
(2)此过程中有多少热量生成?
(3)滑块与木板间的滑动摩擦因数有多大?
“物理1-------2”模块
(1)(在给出的四个选项中,可能只有一个选项正确,也可能有多个选项正确)
根据热力学定律,下列说法正确的是 ( )
A.第二类永动机没有违背能量守恒定律
B.机械能与内能的转化具有方向性
C.气体的扩散现象不具有方向性
D.热机是一种把机械能转化为内能的装置
(2) (在给出的四个选项中,可能只有一个选项正确,也可能有多个选项正确)
由 衰变为
衰变为 要经过x次α衰变和y次β衰变,其中( )
要经过x次α衰变和y次β衰变,其中( )
A.x=6,y="8 " B.x=8,y="6 " C.x=16,y="22 " D.x=22,y=16
(3)质量为0.1 kg,比热为2.0×103 J/(kg·°C)的木块,以4 m/s的初速度在水平桌面上滑行4 m后停下,如果木块克服摩擦力所做的功全部用来使木块的内能增加,这木块温度升高多少?
如图所示,水平传送带的皮带以恒定的速度v运动,一个质量为m小物块以一定的水平初速度v垂直皮带边缘滑上皮带,假设皮带足够大,物块与皮带间的动摩擦因数为μ。

(1)分析说明物块在皮带上做什么运动?
(2)物块在皮带上运动的整个过程中,摩擦力对物块做的功及生的热。
(3)物块在皮带上运动的速度最小值。
“潮汐发电”是海洋能利用中发展最早、规模最大、技术较成熟的一种方式。某海港的货运码头,就是利用“潮汐发电”为皮带式传送机供电,图1所示为皮带式传送机往船上装煤。本题计算中取sin18o=0.31,cos18o=0.95,水的密度ρ =1.0×103kg/m3,g=10m/s2。
(1)皮带式传送机示意图如图2所示, 传送带与水 平方向的角度θ = 18o,传送带的传送距离为L = 51.8m,它始终以v = 1.4m/s的速度运行。在传送带的最低点,漏斗中的煤自由落到传送带上(可认为煤的初速度为0),煤与传送带之间的动摩擦因数μ = 0.4。求:从煤落在传送带上到运至传送带最高点经历的时间t;
平方向的角度θ = 18o,传送带的传送距离为L = 51.8m,它始终以v = 1.4m/s的速度运行。在传送带的最低点,漏斗中的煤自由落到传送带上(可认为煤的初速度为0),煤与传送带之间的动摩擦因数μ = 0.4。求:从煤落在传送带上到运至传送带最高点经历的时间t;
(2)图3为潮汐发电的示意图。左侧是大海,中间
有水坝,水坝下装有发电机,右侧是水库。当涨潮到海平面最高时开闸,水由通道进入海湾水库,发电机在水流的推动下发电,待库内水面升至最高点时关闭闸门;当落潮到海平面最低时,开闸放水发电。设某潮汐发电站发电有效库容V=3.6×10 6m3,平均潮差Δh = 4.8m,一天涨落潮两次,发电四次。水流发电的效率η1= 10%。求该电站一天内利用潮汐发电的平均功率P;
(3)传送机正常运行时,1秒钟有m = 50kg的煤从漏斗中落到传送带上。带动传送带的电动机将输入电能转化为机械能的效率η2= 80%,电动机输出机械能的20%用来克服传送带各部件间的摩擦(不包括传送带与煤之间的摩擦)以维持传送带的正常运行。若用潮汐发电站发出的电给传送机供电,能同时使多少台这样的传送机正常运行?