高中物理常见家用电器技术参数的含义及其选用试题

如图所示，质量为m的滑块，放在光滑的水平平台上，平台右端B与水平传送带相接，传送带的运行速度为v₀，长为L，今将滑块缓慢向左压缩固定在平台上的轻弹簧，到达某处时突然释放，当滑块滑到传送带右端C时，恰好与传送带速度相同。滑块与传送带间的动摩擦因数为μ。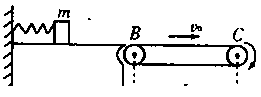

（1）试分析滑块在传送带上的运动情况。
（2）若滑块离开弹簧时的速度大于传送带的速度，求释放滑块时，弹簧具有的弹性势能。
（3）若滑块离开弹簧时的速度大于传送带的速度，求滑块在传送带上滑行的整个过程中产生的热量。

一位身高1.80 m的跳高运动员擅长背越式跳高，他经过25 m弧线助跑，下蹲0.2 m蹬腿、起跳，划出一道完美的弧线，创造出他的个人最好成绩2.39 m（设其重心C上升的最大高度实际低于横杆0.1 m）。如果他在月球上采用同样的方式起跳和越过横杆，请估算他能够跃过横杆的高度为多少？
某同学认为：该运动员在地球表面能够越过的高度H＝＋0.1，则有v₀＝¼
该名运动员在月球上也以v₀起跳，能够越过的高度H’＝＋0.1¼
根据万有引力定律，月球表面的重力加速度为地球表面重力加速度的1/6，所以H’＝¼
你觉得这位同学的解答是否合理？如果是，请完成计算；如果你觉得不够全面，请说明理由，并请用你自己的方法计算出相应的结果。

如图所示，质量为m的物体（可视为质点）以某一速度从A点冲上倾角为30°的固定斜面，其运动的加速度为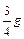，此物体在斜面上上升的最大高度为h，则在这个过程中物体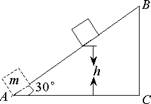

A．重力势能增加了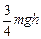

B．重力势能增加了mgh

C．动能损失了mgh

D．机械能损失了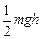

光滑水平地面上叠放着两个物体A和B,如图所示.水平拉力F作用在物体B上,使A、B两物体从静止出发一起运动.经过时间t,撤去拉力F,再经过时间t,物体A、B的动能分别设为E_A和E_B,在运动过程中A、B始终保持相对静止.以下有几个说法：

①E_A+E_B等于拉力F做的功  ②E_A+E_B小于拉力F做的功  ③E_A等于撤去拉力F前摩擦力对物体A做的功  ④E_A大于撤去拉力F前摩擦力对物体A做的功其中正确的是(    )
A.①③     B.①④    C.②③     D.②④

物体在一个不为零的向上的提力作用下参与了下列三种运动：匀速上升、加速上升和减速上升．关于这个物体在这三种情况下机械能的变化情况，正确的说法是   （ ）

A．匀速上升机械能不变，加速上升机械能增加，减速上升机械能减小

B．匀速上升和加速上升机械能增加，减速上升机械能减小

C．三种情况下，机械能均增加

D．由于这个提力和重力大小关系不明确，不能确定物体的机械能的增减情况

如图所示，长为L的长木板水平放置，在木板的A端放置一个质量为m的小物块，现缓慢地抬高A端，使木板以左端为轴转动，当木板转到与水平面的夹角为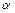时小物块开始滑动，此时停止转动木板，小物块滑到底端的速度为v，则在整个过程中（    ）

A．木板对物块做功为

B．摩擦力对小物块做功为mgLsin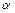

C．支持力对小物块做功为mgLsin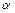

D．滑动摩擦力对小物块做功为

如图所示，半径R＝0.8m的光滑 圆弧轨道固定在光滑水平面上，轨道上方的A有一个可视为质点的质量m＝1kg的小物块，小物块由静止开始下落后打在圆弧轨道的B点，假设在该瞬间碰撞过程中，小物块沿半径方向的分速度立刻减为零，而沿切线方向的分速度不变，此后小物块将沿圆弧轨道下滑，已知A点与轨道圆心O的连线长也为R，且AO连线与水平方向夹角θ＝30°，在轨道末端C点紧靠一质量M＝3kg的长木板，木板上表面与圆弧轨道末端的切线相平，小物块与长木板间的动摩擦因数μ＝0.3，（g取10m/s²）。求：

（1）小物块刚到达B点时的速度大小和方向
（2）要使小物块不画出长木板，木板长度L至少为多少？