高中物理焦耳定律试题

一定值电阻R=10Ω，流过它的电流I=10A。则该电阻的电功率是         W，经过2秒，电阻R生成的焦耳热为        J，经过1小时，电阻消耗电能为        度。

在研究微型电动机的性能时，可采用如图题5所示的实验电路。当调节滑动变阻器R，使电动机停止转动时，电流表和电压表的示数分别为0.5A和1.0V；重新调节R，使电动机恢复正常运转时，电流表和电压表的示数分别为2.0A和15.0V．则当这台电动机正常运转时（   ）

A．电动机的输出功率为8W

B．电动机的输出功率为30W

C．电动机的内阻为2

D．电动机的内阻为7.5

如图所示a电路，当变阻器的滑动片从一端滑动另一端的过程中两电压表的读数随电流表读数的变化情况如图b中的AC.BC两直线所示，不考虑对电路的影响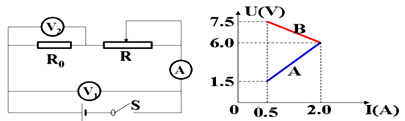

（1）定值电阻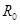，变阻器的总电阻分别为多少？
（2）试求出电源的电动势和内电阻。
（3）变阻器滑动片从一端到另一端的过程中，滑动变阻器消耗的最大电功率为多少？

在研究微型电动机的性能时，应用如图所示的实验电路.当调节滑动变阻器R并控制电动机停止转动时，电流表和电压表的示数分别为0.50 A和2.0 V.重新调节R并使电动机恢复正常运转，此时电流表和电压表的示数分别为2.0 A和24.0 V.则这台电动机正常运转时输出功率为

A．32 W

B．44 W

C．47 W

D．48 W

如图所示，由粗细均匀、同种金属导线构成的正方形线框abcd放在光滑的水平桌面上，线框边长为L，其中ab段的电阻为R。在宽度也为L的区域内存在着磁感应强度为B的匀强磁场，磁场的方向竖直向下。线框在水平拉力的作用下以恒定的速度v通过匀强磁场区域，线框始终与磁场方向垂直且无转动。求：

（1）在线框的cd边刚进入磁场时，bc边两端的电压U_bc；
（2）为维持线框匀速运动，水平拉力的大小F；
（3）在线框通过磁场的整个过程中，bc边金属导线上产生的热量Q_bc。

如图所示，边长为2l的正方形虚线框内有垂直于纸面向里的匀强磁场，一个边长为l的正方形金属导线框所在平面与磁场方向垂直，导线框和虚线框的对角线共线，每条边的材料均相同。从t＝0开始，使导线框从图示位置开始以恒定速度沿对角线方向进入磁场，直到整个导线框离开磁场区域。导线框中的感应电流i(取逆时针方向为正)、导线框受到的安培力F(取向左为正)、导线框中电功率的瞬时值P以及通过导体横截面的电荷量q随时间变化的关系正确的是  

关于电功，下列说法中正确的是（   ）

A．电功的实质是电场力所做的功

B．电功就是电热，两量是一回事

C．电场力做功使金属导体内的自由电子运动的速率越来越大

D．电流通过电动机时的电功率和热功率相等

如图甲所示，一个圆形线圈的匝数n＝100，线圈面积S＝200 cm²，线圈的电阻r＝1 Ω，线圈外接一个阻值R＝4 Ω的电阻，把线圈放入一方向垂直线圈平面向里的匀强磁场中，磁感应强度随时间变化规律如图乙所示。下列说法中正确的是

A．线圈中的感应电流方向为顺时针方向

B．电阻R两端的电压随时间均匀增大

C．前4 s内通过R的电荷量为4×10^－4 C

D．线圈电阻r消耗的功率为4×10^－4 W

如图所示，电源电动势E=10V，其内阻r=1。固定电阻的阻值R₁=3，可变电阻R₂的阻值可在0~20之间调节，电容器的电容C=30μF。求：

(1)闭合开关S，当R₂=1时，求R₂消耗的功率；
(2)在（1）的情况下，电容器上极板所带的电量；
(3)闭合开关S，当R₂取何值时，R₂消耗的功率最大，最大功率为多少。

如图所示，电源电动势E＝30V，内阻r＝1Ω，灯泡上标有“6V 12W”字样，直流电动机线圈电阻R＝2Ω，若灯泡恰好能正常发光，求电动机输出的机械功率．

在一根导线两端加上一定的电压，每秒内发出一定的热量，今将这根导线均匀地拉长为原来的n倍后，再加上同样的电压，则这根导线每秒所产生的热量是原来的______倍。

如图所示，一直流电动机与阻值的电阻串联接在电源上，电源电动势E=20V，内阻，用理想电压表测出电动机两端的电压，已知电动机线圈电阻，则

A．通过电动机的电流为10A

B．电动机的输入功率为100W

C．电动机发热消耗的功率为1W

D．电动机输出的功率为9W

关于三个公式：①P=IU，②P= I²R③P=，下列叙述正确的是（    ）

A．公式①适用于任何电路的热功率

B．公式②适用于任何电路的热功率

C．公式①、②、③适用于任何电路电功率

D．上述说法都不正确

一理想变压器的原、副线圈的匝数比为3:1，在原、副线圈的回路中分别接有阻值相同的电阻，原线圈一侧接在电压为的正弦交流电源上，如图所示。设副线圈回路中电阻两端的电压为，原、副线圈回路中电阻消耗的功率的比值为，则（）

A．		B．
C．		D．

如图（甲），MN、PQ两条平行的光滑金属轨道与水平面成θ = 30°角固定，M、P之间接电阻箱R，电阻箱的阻值范围为0～4Ω，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B = 0.5T。质量为m的金属杆a b水平放置在轨道上，其接入电路的电阻值为r。现从静止释放杆a b，测得最大速度为v_m。改变电阻箱的阻值R，得到v_m与R的关系如图（乙）所示。已知轨距为L = 2m，重力加速度g=l0m/s²，轨道足够长且电阻不计。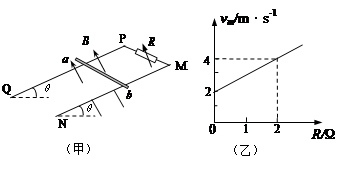

（1）当R = 0时，求杆a b匀速下滑过程中产生感生电动势E的大小及杆中的电流方向；
（2）求金属杆的质量m和阻值r；
（3）求金属杆匀速下滑时电阻箱消耗电功率的最大值P_m。