高中物理焦耳定律试题

在如图所示的电路中，E为电源，其内阻为r，L为小灯泡（其灯丝电阻可视为不变），R₁．R₂为定值电阻，R₃为光敏电阻，其阻值大小随所受照射光强度的增大而减小，V为理想电压表．若将照射R₃的光的强度减弱，则（ ）

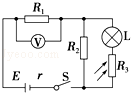
A．电压表的示数变大	B．小灯泡消耗的功率变大
C．通过R2的电流变小	D．电源内阻的功率变小

某一用直流电动机提升重物的装置，如图所示，重物m=50kg，电源的电动势E=110V，不计电源内阻及各处的摩擦．当电动机以v=0.80m/s的恒定速度向上提升重物时，电路中的电流强度为I=5A，（g=10m/s²），下列说法中正确的是（ ）

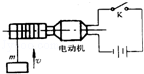
A．电动机线圈的电阻是4Ω

B．电动机的输出功率是400W

C．电动机的输入功率是500W

D．电动机线圈的发热功率是125W

如图所示，有一磁感强度B=0.1T的水平匀强磁场，垂直匀强磁场放置一很长的金属框架，框架上有一导体ab保持与框架边垂直、由静止开始下滑．已知ab长100cm，质量为0.1kg，电阻为0.1Ω，框架电阻不计，取g=10m/s²，求：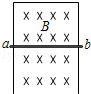

（1）导体ab下落的最大加速度和最大速度；
（2）导体ab在最大速度时产生的电功率．

在如图所示的电路中，R₁是由某金属氧化物制成的导体棒（非纯电阻），实验证明通过它的电流I和它两端电压U遵循I=kU³的规律（式中k=0.02A/V³），R₂是普通电阻，阻值为24Ω，遵循欧姆定律，电源电动势E=6V，闭合开关S后，电流表的示数为0.16A．求：

（1）通过R₁的电流I₁和它两端的电压U₁；
（2）通过R₂的电流I₂和它两端的电压U₂；
（3）R₁、R₂消耗的电功率P₁、P₂；
（4）电源的内电阻r．

用公式R=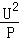求出“220V，40W”灯泡的电阻为1210Ω，而用欧姆表测得其电阻只有90Ω．下列分析正确的是（ ）

A．一定是读数时乘错了倍率

B．可能是测量前没有调零

C．一定是欧姆表坏了

D．1210Ω是灯泡正常工作时较高温度下的电阻，90Ω是灯泡常温下的电阻

“好变频1度到天明”﹣﹣此广告语意为1度电（1kW•h）可使变频空调工作一整夜（以10h计）．同样的1度电可供铭牌如图所示的电扇工作约（ ）

A．1整夜

B．2整夜

C．3整夜

D．4整夜

如图所示，两根光滑的金属导轨，平行放置在倾角为θ的斜面上，导轨的左端接有电阻R，导轨自身的电阻不计，磁场方向垂直于斜面向上，质量为m、电阻不计的金属棒ab在沿着斜面、与棒垂直的恒力F作用下沿导轨匀速上滑h高度，在此过程中（ ）

A．作用于金属棒上的各个力的合力所做的功等于零

B．作用于金属棒上的各个力的合力所做的功等于mgh与电阻R上发出的焦耳热之和

C．恒力F与安培力的合力所的功等于零

D．恒力F与安培力的合力所做的功等于电阻R上发出的焦耳热

如图所示的电路中，R₁=3Ω，R₂=6Ω，R₃=1.5Ω，C=20μF当开关S断开时，电源所释放的总功率为2W；当开关S闭合时，电源所释放的总功率为4W求：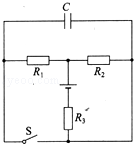

（1）电源的电动势和内电阻；
（2）闭合S时，电源的输出功率；
（3）S断开和闭合时，电容器所带的电荷量各是多少？

在如图所示的电路中，当滑动变阻器的滑动片向下移动时，关于电灯L的亮度及电容器C所带电荷量Q的变化判断正确的是（ ）

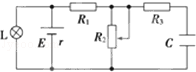
A．L变暗，Q增大

B．L变暗，Q减小

C．L变亮，Q增大

D．L变亮，Q减小

在某段电路中，其两端电压为U，通过的电流为I，通电时间为t，若该电路电阻为R，则关于电功和电热的关系，下列结论不正确的是（ ）

A．在任何电路中，电功W=UIt=I^2Rt

B．在任何电路中，电功为UIt，电热为I^2Rt

C．在纯电阻电路中，UIt=I^2Rt

D．在非纯电阻电路中，UIt＞I^2Rt

如图所示，直流电动机M串联在直流电路中，其轴与圆盘中心O相连．开关S断开时，电压表的读数12.6V，开关S接通时，电流表的读数为2A，电压表的读数为12V．圆盘半径为5cm，测速计测得圆盘的转速为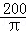r/s，两弹簧秤的读数分别为F₁=7N，F₂=6.10N，问：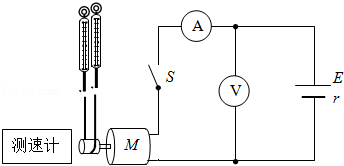

（1）电动机的输出功率、效率各为多少？
（2）拉紧皮带可使电动机停转，此时电压表、电流表的读数各为多少？电动机的输入功率为多大？

关于电功和电热的计算，下列说法正确的是（ ）

A．如果是纯电阻电路，电功可用公式W=UIt计算，也可用公式W=I^2Rt计算

B．如果是纯电阻电路，电热可用公式W=I^2Rt计算，但不能用公式W=UIt计算

C．如果不是纯电阻电路，电功只能用公式W=I^2Rt计算

D．如果不是纯电阻电路，电热可用公式W=I^2Rt计算，也可用公式W=UIt计算

如图所示电路，电灯R₁=24Ω，电动机绕组的电阻R₀=1Ω，当电键S₁、S₂闭合时，测得电阻R₁的电功率是P=96W，理想电流表的读数为I=5A，求此时：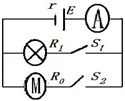

（1）电源的输出功率；
（2）电动机的输出功率．

如图甲，MN、PQ两条平行的光滑金属轨道与水平面成θ=37°角固定，M、P之间接电阻箱R，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B=0.5T．质量为m的金属杆a b水平放置在轨道上，其接入电路的电阻值为r．现从静止释放杆a b，测得最大速度为v_m．改变电阻箱的阻值R，得到v_m与R的关系如图乙所示．已知轨距为L=2m，重力加速度g取l0m/s²，轨道足够长且电阻不计．求：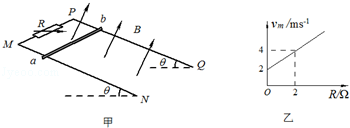

（1）杆a b下滑过程中感应电流的方向及R=0时最大感应电动势E的大小；
（2）金属杆的质量m和阻值r；
（3）当R=4Ω时，求回路瞬时电功率每增加1W的过程中合外力对杆做的功W．

如图所示，直线A为某电源的U﹣I图线，曲线B为某小灯泡D₁的U﹣I图线的一部分，用该电源和小灯泡D₁组成闭合电路时，灯泡D₁恰好能正常发光，则下列说法中正确的是（ ）

A．此电源的内阻为Ω

B．灯泡D1的额定电压为3V，功率为6W

C．把灯泡D1换成“3V，20W”的灯泡D2，电源的输出功率将变大

D．由于小灯泡B的U﹣I图线是一条曲线，所以灯泡发光过程，欧姆定律不适用