高中物理焦耳定律试题

如图所示的电路中，两平行金属板A、B水平放置，极板长L="80" cm，两板间的距离d="40" cm。电源电动势E=40V，内电阻r=lΩ，电阻R=15Ω，闭合开关S，待电路稳定后，将一 带负电的小球从B板左端且非常靠近B板的位置以初速度vo="4" m／s水平向右射入两板间，该小球可视为质点。若小球带电量 q=l×10^-2C，质量为 m=2×10^-2kg，不考虑空气阻力，电路中电压表、电流表均是理想电表。若小球恰好从A板右边缘射出（g取10 m／s²）。求：

(1)滑动变阻器接入电路的阻值为多少？
(2)此时电流表、电压表的示数分别为多少？
(3)此时电源的输出功率是多少？

在如图电路中，电源电动势E＝6V，内阻r＝1Ω，保护电阻R₀＝3Ω，滑动变阻器总电阻R＝20Ω，闭合电键S，在滑片P从a滑到b的过程中，若安培表内阻忽略，正确的是（   ）

A．安培表的示数先减小后增大

B．安培表的示数先增大后减小

C．滑动变阻器消耗的功率先增大后减小

D．滑动变阻器消耗的功率先增大后减小，再增大后减小

如图所示，和的规格为“4W、100Ω”，的规格为“1W、100Ω”，当A、B端加电源通电时，这部分电路允许消耗的最大功率为（  ）

A.1.25W      B.1.5W       C.3W         D.9W

如图所示，导体杆OP可绕O轴沿半径为r的光滑的半圆形框架在匀强磁场中以角速度ω转动，磁感应强度为B，AO间接有电阻R，杆和框架电阻不计，则所施外力的功率为（       ）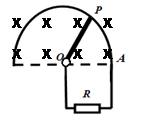

A．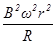

B．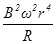

C．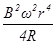

D．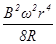

如图所示电路中，三个相同的灯泡额定功率是40 W，在不损坏灯泡的情况下，这三个灯泡消耗的总功率最大不应超过 （  ）

A．40 W

B．60 W

C．80 W

D．120 W

利用电动机通过如图所示的电路提升重物，已知电源电动势E＝6 V，电源内阻r＝1 Ω，电动机内阻r₀＝2Ω，电阻R＝3 Ω，重物质量m＝0.10 kg.当电动机以稳定的速度匀速提升重物时，电压表的示数为U="5.5" V。不计空气阻力和摩擦，取g=" 10" m/s²。求：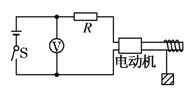

（1）电源内电压U₁；
（2）重物匀速上升时的速度v。

如图虚线框内为高温超导限流器，它由超导部件和限流电阻并联组成。超导部件有一个超导临界电流I_C，当通过限流器的电流I>I_C时，将造成超导体失超，从超导态(电阻为零，即R₁=0)转变为正常态(一个纯电阻，且R₁ ="3Ω" )，以此来限制电力系统的故障电流。已知超导临界电流I_C="1.2" A，限流电阻R₂ =6Ω，小灯泡L上标有“6 V 6 W”的字样，电源电动势E="8" V，内阻r=2Ω。原来电路正常工作，超导部件处于超导态，灯泡L正常发光，现L突然发生短路，则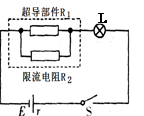

A．灯泡L短路前通过R2的电流为A

B．灯泡L短路后超导部件将由超导状态转化为正常态，通过灯泡电流为零

C．灯泡L短路后通过R1的电流为4 A

D．灯泡L短路后通过R2的电流为A

如图所示，电源电动势E=10V，其内阻r=1。固定电阻的阻值R₁=3，可变电阻R₂的阻值可在0~20之间调节，电容器的电容C=30μF。求：

(1)闭合开关S，当R₂=1时，求R₂消耗的功率；
(2)在（1）的情况下，电容器上极板所带的电量；
(3)闭合开关S，当R₂取何值时，R₂消耗的功率最大，最大功率为多少。

如图所示，电源电动势E＝30V，内阻r＝1Ω，灯泡上标有“6V 12W”字样，直流电动机线圈电阻R＝2Ω，若灯泡恰好能正常发光，求电动机输出的机械功率．

在一根导线两端加上一定的电压，每秒内发出一定的热量，今将这根导线均匀地拉长为原来的n倍后，再加上同样的电压，则这根导线每秒所产生的热量是原来的______倍。

如图所示，一直流电动机与阻值的电阻串联接在电源上，电源电动势E=20V，内阻，用理想电压表测出电动机两端的电压，已知电动机线圈电阻，则

A．通过电动机的电流为10A

B．电动机的输入功率为100W

C．电动机发热消耗的功率为1W

D．电动机输出的功率为9W

关于三个公式：①P=IU，②P= I²R③P=，下列叙述正确的是（    ）

A．公式①适用于任何电路的热功率

B．公式②适用于任何电路的热功率

C．公式①、②、③适用于任何电路电功率

D．上述说法都不正确

如图所示，在磁感应强度B=1.0T的匀强磁场中，金属杆PQ在外力F作用下在粗糙U型导轨上以速度v=2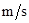向右匀速滑动，两导轨间距离L=1.0m，电阻R=3.0，金属杆的电阻r=1.0，导轨电阻忽略不计，则下列说法正确的是（  ）

A．通过的感应电流的方向为由d到a

B．金属杆PQ切割磁感线产生的感应电动势的大小为2.0 V

C．金属杆PQ受到的安培力大小为0.5 N

D．外力F做功大小等于电路产生的焦耳热

如图甲所示，不变形、足够长、质量为m₁=0.2kg的“U”形金属导轨PQMN放在绝缘水平桌面上，QP与MN平行且距离d=1m，Q、M间导体电阻阻值R=4Ω，右内侧紧靠两固定绝缘小立柱1、2；光滑金属杆KL电阻阻值r=1Ω，质量m₂=0.1kg，垂直于QP和MN，与QM平行且距离L=0.5m，左侧紧靠两固定绝缘小立柱3、4。金属导轨与桌面的动摩擦因数μ=0.5，最大静摩擦力等于滑动摩擦力，其余电阻不计。从t=0开始，垂直于导轨平面的磁场磁感应强度如图乙所示。

（1）求在整个过程中，导轨受到的静摩擦力的最大值f_max；
（2）如果从t=2s开始，给金属杆KL水平向右的外力，外力对金属杆作用的功率保持不变为P₀=320W，杆到达最大速度时撤去外力，求撤去外力后QM上产生的热量Q_R=？

如图（甲），MN、PQ两条平行的光滑金属轨道与水平面成θ = 30°角固定，M、P之间接电阻箱R，电阻箱的阻值范围为0～4Ω，导轨所在空间存在匀强磁场，磁场方向垂直于轨道平面向上，磁感应强度为B = 0.5T。质量为m的金属杆a b水平放置在轨道上，其接入电路的电阻值为r。现从静止释放杆a b，测得最大速度为v_m。改变电阻箱的阻值R，得到v_m与R的关系如图（乙）所示。已知轨距为L = 2m，重力加速度g=l0m/s²，轨道足够长且电阻不计。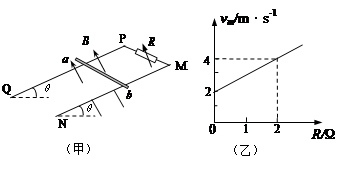

（1）当R = 0时，求杆a b匀速下滑过程中产生感生电动势E的大小及杆中的电流方向；
（2）求金属杆的质量m和阻值r；
（3）求金属杆匀速下滑时电阻箱消耗电功率的最大值P_m。