如图所示,匀强电场中A、B、C三点构成一个直角三角形,把电荷量 C的点电荷由A点移动到B点,电场力做功
C的点电荷由A点移动到B点,电场力做功 J,再由B点移到C点电荷克服电场力做功
J,再由B点移到C点电荷克服电场力做功 J,取B点的电势为零,
J,取B点的电势为零,
求(1)A、C两点的电势 (2)场强的方向.
在竖直平面内建立xoy直角坐标系,oy表示竖直向上方向.如图所示.已知该平面内存在沿x轴正向的区域足够大的匀强电场.一带电小球从坐标原点o沿ox方向以4J的初动能竖直向上抛出.不计空气阻力,它到达的最高位置如图中M点所示.求:(1)小球在M点时的动能EkM.
(2)设小球落回跟抛出点在同一水平面时的位置为N,求小球到达N点时的动能EkN.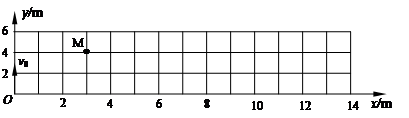
(12)如下图所示,一对平行金属极板相距d=2cm,两板间匀强电场方向向下,场强大小E=1.6×103v/m,其中下极板接地(零电势)。A点距下板为h1=1.5cm,B板距下板为h2=0.5cm,试求:(电子电荷量为e=-1.6×10-19C)
(1)两金属板之间的电势差大小;
(2)将一个电子从A点移动到B点电场力做的功?
电子的电势能是增加还是减少?
为使带负电的点电荷q在一匀强电场中沿直线匀速地由A运动到B,必须对该电荷施加一个恒力F,如图所示,若AB="0.4" m,α=37°,q=-3×10-7 C,F=1.5×10-4 N,A点的电势UA="100" V.(不计负电荷受到的重力)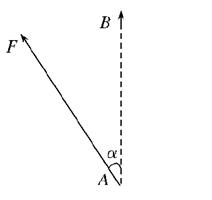
(1)在图中用实线画出电场线,用虚线画出通过A、B两点的等势线,并标明它们的电势.
(2)求q在由A到B的过程中电势能的变化量是多少?
如图所示,绝缘水平板面上,相距为L的A、B两个点分别固定着等量正点电荷.O为AB连线的中点,C、D是AB连线上的两点,AC=CO=OD=OB=1/4L.一质量为m、电量为+q的小滑块(可视为质点)以初动能E0从C点出发,沿直线AB向D运动,滑动第一次经过O点时的动能为nE0(n>1),到达D点时动能恰好为零,小滑块最终停在O点,求:
(1)小滑块与水平板面之间的动摩擦因数μ;
(2)OD两点间的电势差UOD;
(3)小滑块运动的总路程s.
如图所示,在水平向右的、强度E = 2000V/m的匀强电场中,质量m = 1.73毫克的带电粒子以大小v0 = 10m/s、方向和水平方向成30°的初速度从A点射入,发现它恰能做直线运动。以A点所在的等势面为参考平面,电场区域足够大,试求:
(1)粒子的电性和电量;
(2)粒子沿直线前进的最大距离;
(3)粒子可以获得的最大电势能。
(16分)如图10所示,在水平向左的匀强电场中,一带电小球用绝缘轻绳(不伸缩)悬于O点,平衡时小球位于A点,此时绳与竖直方向的夹角θ=53°,绳长为l,B、C、D到O点的距离均为l,BD水平,OC竖直.BO=CO=DO=l.
(1)将小球移到B点,给小球一竖直向下的初速度vB,小球
到达悬点正下方C点时绳中拉力恰等于小球重力,求vB的大小.
(2)当小球移到D点后,让小球由静止自由释放,求:小球首次经过悬点O正下方时的速率.(计算结果可带根号,取sin53°=0.8)
(12分)一个不带电的金属板,表面有很薄的光滑绝缘层,与水平方向成θ角放置.金属板上B、C两点间的距离为L,在金属板上方的A点固定一个带电荷量为+Q的点电荷,金属板处在+Q的电场中.已知A、B、C三点在同一竖直平面内,且AB水平,AC竖直,如图所示.将一个带电荷量为+q(q  Q,q对原电场无影响)可看做点电荷的小球,从B点无初速释放,如果小球质量为m,下滑过程中带电荷量不变,求:
Q,q对原电场无影响)可看做点电荷的小球,从B点无初速释放,如果小球质量为m,下滑过程中带电荷量不变,求:
(1)小球在B点的加速度;
(2)下滑到C点时的速度.
如图 所示,在匀强电场中,有A、B两点,它们间的距离为2 cm,两点的连线与场强方向成60°角.将一个电荷量为-2×10-5 C的电荷由A移到B,其电势能增加了0.1 J.问:
(1)在此过程中,电场力对该电荷做了多少功?
(2)A、B两点的电势差UAB为多大?
(3)匀强电场的场强为多大?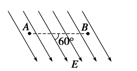
在电场强度为E的匀强电场中,有两个质量均为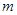 的带电小球,带电量分别为
的带电小球,带电量分别为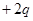 和
和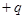 ,两小球用长为
,两小球用长为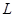 的绝缘线相连,另用一根绝缘线系住带电为
的绝缘线相连,另用一根绝缘线系住带电为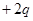 的小球悬挂在O点而处于平衡状态,如图11所示。重力加速度为g。试确定:
的小球悬挂在O点而处于平衡状态,如图11所示。重力加速度为g。试确定:
(1)若电场方向竖直向下,悬线对悬点的作用力为多大?
(2)若电场水平向右,两段细线与竖直方向的夹角分别为多大?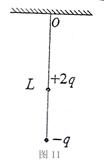
均匀导线制成的单匝正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m。将其置于磁感强度为B的水平匀强磁场上方h处,如图所示。线框由静止自由下落,线框平面保持在坚直平面内,且cd边始终与水平的磁场边界平行。当cd边刚进入磁场时,求:dysz
(1)cd两点哪点电势高,求线框中产生的感应电动势大小;
(2)cd两点间的电势差大小;
(3)若此时线框加速度恰好为零,求线框下落的高度h所应满足的条件。
如图,绝缘的光滑圆弧曲面固定在竖直平面内,B为曲面最低点.曲面上的A点与曲面圆心O的连线与竖直方向成夹角θ=37°.曲面所在区域和B点左下方的区域内都存在电场强度大小都为E的匀强电场,方向分别是水平向右和竖直向上.开始时有一质量为m的带电小球处于A点恰好保持静止.此后将曲面内的电场撤去,小球沿曲面下滑至B点时以大小为v0的速度水平抛出,最后落在电场内地面的P点,P点与B点间的水平距离为L. 已知tan37°=0.75,重力加速度为g,求:
(1)小球的带电性及电荷量q.
(2)小球运动到P点瞬间的速度vP的大小.
如图所示,在光滑绝缘水平面上B点的正上方O处固定一个质点,在水平面上的A点放另一个质点,两个质点的质量均为m,带电量均为+Q。C为AB直线上的另一点(O、A、B、C位于同一竖直平面上),AO间的距离为L,AB和BC间的距离均为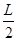 ,在空间加一个水平方向的匀强电场后A处的质点处于静止。试问:
,在空间加一个水平方向的匀强电场后A处的质点处于静止。试问: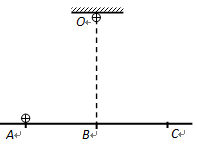
(1)该匀强电场的场强多大?其方向如何?
(2)给A处的质点一个指向C点的初速度,该质点到达B点时所受的电场力多大?
(3)若初速度大小为v0,质点到达C点时的加速度和速度分别多大?
如图所示的电场,等势面是一簇互相平行的竖直平面,间隔均为d,各面电势已在图中标出,现有一质量为m的带电小球以速度v0,方向与水平方向成45°角斜向上射入电场,要使小球做直线运动.问:
小球应带何种电荷?电荷量是多少?
在入射方向上小球最大位移量是多少?(电场足够大)
如图所示,A、B、C是匀强电场中的三点,已知 A="10" V,
A="10" V, B ="4" V,
B ="4" V, C=-2 V,∠A=30°,∠B=90°,AC=4
C=-2 V,∠A=30°,∠B=90°,AC=4 cm,试确定:
cm,试确定:
该电场中的一条电场线.
场强E的大小.