高中物理电势试题

（1）经多长时间两球发生第一次碰撞？碰撞前小球A的速度为多大？
（2）在以后的各次碰撞中，相邻两次碰撞间隔的时间是否相等（如相等，为多少；如不等，说理由）？
（3）从加上电场起计时，经多长时间小球A以多大的速度与小球B发生第3次碰撞？

一质量为m=6kg带电量为q= -0.1C的小球P自动摩擦因数u=0.5倾角θ=53°的粗糙斜面顶端由静止开始滑下，斜面高h=6.0m，,斜面底端通过一段光滑小圆弧与一光滑水平面相连。整个装置处在水平向右的匀强电场中,场强E=200N/C，忽略小球在连接处的能量损失，当小球运动到水平面时，立即撤去电场。水平面上放一静止的不带电的质量也为m的1/4圆槽Q，圆槽光滑且可沿水平面自由滑动，圆槽的半径R=3m,如图所示。（sin53°="0.8" ，cos53°="0.6" ，g=10m/s2。）

（1）在沿斜面下滑的整个过程中,P球电势能增加多少？
（2）小球P运动到水平面时的速度大小。
（3）试判断小球P能否冲出圆槽Q。

如图8－1所示，实线是一个电场中的电场线，虚线是一个负检验电荷在这个电场中的轨迹，若电荷是从a处运动到b处，以下判断正确的是：              [    ]

A．电荷从a到b加速度减小

B．b处电势能大

C．b处电势高

D．电荷在b处速度小

如图所示，竖直平面内光滑圆弧形管道MC半径为R，它与水平管道CD恰好相切。水平面内的等边三角形ABC的边长为L，顶点C恰好位于圆周最低点，CD是AB边的中垂线。在A、B两顶点上放置一对等量异种电荷，各自所带电荷量为q。现把质量为m、带电荷量为＋Q的小球（小球直径略小于管道内径）由圆弧形管道的最高点M处静止释放，不计＋Q对原电场的影响以及带电荷量的损失，取无穷远处为零电势，静电力常量为k，重力加速度为g，则

A．D点的电场强度大于C点
B．D点的电势大于C点
C．小球在管道中运动时，机械能不守恒
D．小球对圆弧形管道最低点C处的压力大小为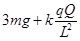

如图所示，A、B、C表示匀强电场中的三点，它们的电势分别为φA="-5" V,φB="9" V,φC="2" V.试在图中画出过A、B、C点的三条等势线，并画出一条过C点的电场线.

在场强大小为E的匀强电场中，一质量为m、带电量为＋q的物体以某一初速度沿电场的反方向做匀减速直线运动，其加速度大小为0.8Eq／m，物体运动距离S时速度减小为零。则物体的电势能     了        ，机械能        了         。

一个带正电荷的质点，电荷量q=2.0×10-9 C，在静电场中由a点移到b点，在此过程中，除电场力做功外，其他力做功为6.0×10-5 J，质点的动能增加了8.0×10-5 J.则ab两点间电势差Uab为（   ）

A．3.0×104 V	B．1.0×104 V
C．4.0×104 V	D．7.0×104 V

如图甲所示，Q₁、Q₂是两个固定的点电荷，一带正电的试探电荷仅在电场力作用下以初速度v_a沿两点电荷连线的中垂线从a点向上运动，其v-t图象如图乙所示，下列说法正确的是

A．两点电荷一定都带负电，但电量不一定相等

B．两点电荷一定都带负电，且电量一定相等

C．试探电荷一直向上运动，直至运动到无穷远处

D．t2时刻试探电荷的电势能最大，但加速度不为零

如图所示，在竖直平面内，光滑绝缘直杆AC与半径为R的圆周交于B、C两点，在圆心处有一固定的正点电荷，B点为AC的中点，C点位于圆周最低点．现有一质量为m、电荷量为q套在杆上的带负电小球（可视为质点）从A点由静止开始沿杆下滑．已知重力加速度为g，A点距过C点的水平面的竖直高度为3R，小球滑到B点时的速度大小为2．求：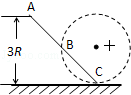

（1）小球滑至c点时的速度的大小；
（2）A、B两点间的电势差；
（3）若以C点做为参考点（零电势点），试确定A点的电势．

如图所示x轴上各点的电场强度如图所示，场强方向与x轴平行，规定沿x轴正方向为正。一负点电荷从坐标原点O以一定的初速度沿x轴正方向运动，点电荷到达x₂位置速度第一次为零，在x₃位置第二次速度为零，不计粒子的重力．下列说法正确的是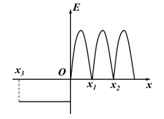

A．点电荷从O点运动到x2，再运动到x3的过程中，速度先均匀减小再均匀增大，然后减小再增大

B．点电荷从O点运动到x2，再运动到x3的过程中，加速度先减小再增大，然后保持不变

C．O点与x2和O点与x3电势差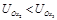

D．点电荷在x2、x3位置的电势能最大

如图所示，空间的虚线框内有匀强电场，AA′、BB′、CC′是该电场的三个等势面，相邻等势面间的距离均为0.5cm，其中BB'为零势能面．一个质量为m，带电量为+q的粒子沿AA′方向以初动能E_k自图中的P点进入电场，刚好从C′点离开电场．已知PA′=2cm．粒子的重力忽略不计．下列说法中正确的是（ ）

A．该粒子通过等势面BB'时的动能是1.25Ek

B．该粒子到达C′点时的动能是2Ek

C．该粒子在P点时的电势能是Ek

D．该粒子到达C′点时的电势能是-0.5Ek

如图所示，长为2L的平板绝缘小车放在光滑水平面上，小车两端固定两个绝缘的带电小球A和B。A、B所带电荷量分别为＋2q和 3q．小车（包括带电小球A、B）的总质量为m。虚线MN与PQ平行且相距3L，开始时虚线MN位于小车正中间。若视带电小球为质点，在虚线MN、PQ间加上方向水平向右、场强大小为E的匀强电场后，小车开始运动。试求：

（1）小车向右运动的最大距离；
（2）此过程中小球B电势能的变化量；
（3）小球A从开始运动至刚离开电场所用的时间。

如图所示，竖直平面内光滑圆弧形管道OMC半径为R，它与水平管道CD恰好相切。水平面内的等边三角形ABC的边长为L，顶点C恰好位于圆周最低点，CD是AB边的中垂线。在A、B两顶点上放置一对等量异种电荷，各自所带电荷量为q。现把质量为m、带电荷量为＋Q的小球（小球直径略小于管道内径）由圆弧形管道的最高点M处静止释放，不计＋Q对原电场的影响以及带电荷量的损失，取无穷远处为零电势，静电力常量为k，重力加速度为g，则

A．D点的电场强度大于C点
B．D点的电势大于C点
C．小球在管道中运动时，机械能不守恒
D．小球运动到圆弧形管道最低点C处时的电场力大小为

如图所示为某示波管内的聚焦电场，实线和虚线分别表示电场线和等势线。则

A．场强Ea>Eb，Eb>Ec

B．电势a>b，c>b

C．沿cba路径移动质子与电子，电荷的电势能改变是一样的

D．沿bc方向直线射入的电子有可能做曲线运动

如图，同一竖直线的A、B两点固定有等量异种点电荷，电量为q，正负如图所示，ΔABC为一等边三角形(边长为L)，CD为高且与右侧竖直光滑1/4圆弧轨道的最低点C相切，已知圆弧的半径为R，现把质量为m带电量为+Q的小球(可视为质点)由圆弧的最高点M静止释放，到最低点C时速度为V₀。已知静电力恒量为k，现取D为电势零点，求：
（1）在等量异种电荷A、B的电场中，M点的电势φ_M?
（2）在最低点C轨道对小球的支持力F_N多大？