高中物理* 用三角函数表示简谐运动实验题

（1）在“用单摆测定重力加速度”的实验中，当单摆做简谐运动时，用秒表测出单摆做n次（一般为30次～50次）全振动所用的时间t，算出周期；用米尺量出悬线的长度L，用游标卡尺测量摆球的直径d，则重力加速度g＝______（用题中所给的字母表达）．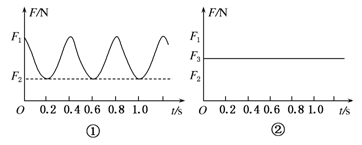

（2）将一单摆挂在测力传感器的探头上，用测力探头和计算机组成的实验装置来测定单摆摆动过程中摆线受到的拉力（单摆摆角小于5°），计算机屏幕上得到如图①所示的F－t图像．然后使单摆保持静止，得到如图②所示的F－t图像．那么：
①此单摆的周期T为__________s；②设摆球在最低点时E_p＝0，已测得当地重力加速度为g，单摆的周期用T表示，那么测得此单摆摆动时的机械能E的表达式是_________    （用字母表示）．

细绳的一端在外力作用下从t=0时刻开始做简谐运动，激发出一列简谐横波。在细绳上选取15个点，图７中第一个图为t=0时刻各点所处的位置，图７中第二个图为t=T/4时刻的波形图（T为波的周期）。在图７中第三个图中画出t=3T/4时刻的波形图。

简谐运动的振动图线可用下述方法画出：如图(1)所示，在弹簧振子的小球上安装一枝绘图笔P，让一条纸带在与小球振动方向垂直的方向上匀速运动，笔P在纸带上画出的就是小球的振动图象．取振子水平向右的方向为振子离开平衡位置的位移正方向，纸带运动的距离代表时间，得到的振动图线如图(2)所示．
①刚开始计时时，振子处在     位置（填左边最大位移处或右边最大位移处），t＝17 s时振子相对平衡位置的位移是      cm，此时速度为        （填正或负）向最大。
②若纸带运动的速度为2 cm/s，振动图线上1、3两点间的距离是       cm。

如图所示，两木块A和B叠放在光滑水平面上，质量分别为m和M，A与B之间的最大静摩擦力为f，B与劲度系数为k的轻质弹簧连接构成弹簧振子。为使A和B在振动过程中不发生相对滑动，则它们的振幅不能大于              ，它们的最大加速度不能大于               。

（1）一列沿着轴正方向传播的横波，在时刻的波形如图甲所示。图甲中某质点的振动图象如图乙所示。质点的振幅是，振动周期为，图乙表示质点(从质点、、、中选填)的振动图象。该波的波速为。

（2）惯性系中有一边长为l的正方形(如图A所示)，从相对系沿方向以接近光速匀速飞行的飞行器上测得该正方形的图象是 。

（3）描述简谐运动特征的公式是＝。自由下落的篮球缓地面反弹后上升又落下。若不考虑空气阻力及在地面反弹时的能量损失，此运动　 (填"是"或"不是")简谐运动。

如图1-1-9所示，小球被套在光滑的水平杆上，跟弹簧相连组成弹簧振子，小球在平衡位置O附近的A、B间往复运动，以O为位移起点，向右为位移x的正方向，则

图1-1-9
（1）速度由正变成负的位置在___________.
（2）位移方向改变的位置在___________，负向最大值的位置在___________.

如图11-1-9所示为一弹簧振子的振动图象，规定向右的方向为正方向，试根据图象分析以下问题：

图11-1-9                 图11-1-10
（1）如图11-1-10所示的振子振动的起始位置是________，从初始位置开始，振子向________（填“右”或“左”）运动.
（2）在图11-1-10中，找出图象中的O、A、B、C、D各对应振动过程中的哪个位置？即O对应_________，A对应_________，B对应_________，C对应________，D对应________.
（3）在t="2" s时，振子的速度的方向与t=0时速度的方向_________.
（4）质点在前4 s内的位移等于_________.

甲、乙两弹簧振子质量相等，其振动图象如图11-1-7所示，则它们振动的机械能大小关系是E_甲_________E_乙（填“＞”“＝”或“＜”）；振动频率的大小关系是f_甲_________f_乙；在0—4 s内，甲的加速度为正向最大的时刻是____________，乙的速度为正向最大的时刻是____________.

图11-1-7

对于弹簧振子的周期性振动，我们可以通过如图11-1-11所示的小球的匀速圆周运动的投影来模拟。即振子从距平衡位置A处静止释放的同时，球恰从B点做匀速圆周运动，小球运动在x轴上的投影与振子运动同步，小球运动的线速度沿x轴的投影即为振子在投影处的速度。圆周运动的周期为T半径为R。由以上条件可知匀速圆周运动的线速度v₁=________,振子在O点的速度大小为__________。

图11-1-11

一弹簧振子的质量为100 g，弹簧的劲度系数为k="10" N/m，将振子拉离平衡位置2 cm处放手使其振动，则此振子振动过程中受到的最大回复力大小是___________N,最大加速度的大小是___________m/s².

甲、乙两个做简谐运动的弹簧振子，在甲振动20次的时间里，乙振动了40次，则甲、乙振动周期之比为___________________；若甲的振幅增大而乙的不变，则甲、乙振动频率之比为______________.

一个做简谐振动的质点，它的振幅是4 cm，频率是2.5 Hz，若从平衡位置开始计时，则经过2 s，质点完成了______________次全振动，质点运动的位移是______________，通过的路程是______________.

一个振子在平衡位置O点附近做简谐运动，它离开O点2.5 s，第一次到达位置P，又经过2 s后，第二次经过位置P，那么再经过____________ s后，它第三次到达P点.

弹簧振子从距离平衡位置5 cm处由静止释放，4 s内完成5次全振动，则这个弹簧振子的振幅为_____________cm，振动周期为_____________s，频率为_____________Hz，4 s末振子的位移大小为_____________cm，4 s内振子运动的路程为_____________cm，若其他条件都不变，只是使振子改为在距平衡位置2.5 cm处由静止释放，该振子的周期为_______s.

已知某人心电图记录仪的出纸速度(纸带的移动速度)是2.5cm/s．如图所示是用此仪器记录下的某人的心电图。(图中每个格的边长为O.5cm)。(1)由图可知此人的心率是_____________次/分，它的心脏每跳一次所需时间是_____________s