高中物理万有引力定律及其应用综合题

宇航员在某星球表面，将一小球从离地面h高处以初速v₀水平抛出，测出小球落地点与抛出点间的水平位移为s.若该星球的半径为R，引力常量为G，求该星球的密度为多大.

计算下列物体间的万有引力大小：
（1）两个质量各为50 kg的均匀球相距1 m远；
（2）太阳质量M=2.0×10³⁰kg，地球的质量M=6.0×10²⁴kg，太阳与地球相距R=1.5×10¹¹m.

如果把地球绕太阳公转看作是匀速圆周运动，轨道平均半径约为1.5×10⁸ km，已知万有引力常量G=6.67×10^-11N·m²/kg²，则可估算出太阳的质量大约是多少？（结果取一位有效数字）

两个行星质量分别为m₁和m₂，绕太阳运行的轨道半径分别是r₁和r₂，求:
（1）它们与太阳间的万有引力之比；
（2）它们的公转周期之比.

设想有一宇航员在某行星的极地上着陆时，发现在当地的重力是同一物体在地球上重力的0.01倍，而该行星一昼夜的时间与地球相同，物体在它的赤道时恰好失重.若存在这样的星球，它的半径R应是多大?

在月球上以初速度v₀竖直上抛一个小球，经过时间t落回到抛出点，已知月球的半径为R，试求月球的质量.

月球质量是地球质量的，月球半径是地球半径的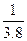，在距月球表面14m高处，有一质量m="60" kg的物体自由下落．
（1）它落到月球表面需要多长时间？
（2）它在月球上的重力和质量跟在地球上是否相同？（已知地球表面的重力加速度g_地=9．8m/s²）

宇航员站在一星球表面上的某高处，沿水平方向抛出一个小球，经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L，若抛出时的初速度增大2倍，则抛出点与落地点之间的距离为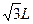.已知两落地点在同一水平面上，该星球的半径为R，万有引力常量为G，求该星球的质量M.

半径为R、质量为M的铅球内有一半径为R/2的球形空腔，空腔表面与铅球面内切，求这个空腔铅球以多大的力吸引质量为m的小球（体积不计）．已知小球离铅球中心的距离为d，且在铅球中心与空腔中心的连线上，如图所示．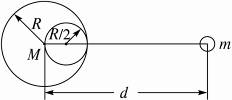

某行星昼夜转动时间T₀=8h，若用一弹簧测力计去测量同一物体的重力，结果在行星赤道上比它在两极处小9﹪.设想该行星自转角速度加快,在赤道上的物体将完全失重.则此行星自转周期多大?(行星看作标准球体)

如右图所示，火箭内平台上放有测试仪器，火箭从地面启动后，以加速度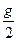竖直向上匀加速运动，升到某一高度时，测试仪对平台的压力为启动前压力的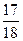．已知地球半径为R，求火箭此时离地面的高度．（g为地面附近的重力加速度）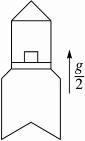

两个质量均为m的星体，其连线的中垂线为MN，O为连线的中点，一质量为m的物体从O沿OM方向运动，则它受的万有引力如何变化？

某个行星的质量是地球质量的一半，半径也是地球的一半，若某人在地球上能举起质量为150kg的重物，则在该行星上该人最多能举起质量为多少的物体？

已知月球的质量是地球质量的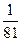，月球半径是地球半径的，在离月球表面38 m处让质量为m="60" kg的物体自由下落.求：
（1）月球表面的重力加速度；
（2）物体下落到月球表面所用的时间；
（3）物体在月球上的质量和“重力”与在地球上的是否相同.（已知地球表面重力加速度g_地="9.8" m/s²）

已知地球的半径R≈6.4×10⁶m,地球表面的重力加速度g≈10m/s²,万有引力恒量G≈6.7×10^-11N·kg²/m²。由此推导并估算：（把结果只保留一位有效数字即可）
（1）地球的质量M约为多少?
（2）近地环绕卫星的最大线速度v₁约为多少?