卡文迪许把他自己的实验说成是“称地球的重量”（严格地说应是“测量地球的质量”）。如果已知引力常量G、地球半径R和重力加速度g，那么我们就可以计算出地球的质量M= ；如果已知某行星绕太阳运行所需的向心力是由太阳对该行星的万有引力提供的，该行星做匀速圆周运动，只要测出 和 就可以计算出太阳的质量。
一星球的半径为R，为了测量该星球两极和赤道的重力加速度及星球自转角速度，某人用小球在该星球表面做了以下实验：（不计小球在运动的过程中所受阻力）
①在该星球的两极（相当于地球的南极和北极），以初速度v0（相对地面）从h高处将一小球水平抛出，小球触地时速度与水平方向成α角．则测量的该星球两极的重力加速度为 ；
②在该星球的赤道上（相当于地球的赤道），同样以速度v0（相对地面）从h高处将一小球水平抛出，小球触地时速度与水平方向成β角．该星球赤道上的重力加速度为 ；该星球的自转角速度为 ．
如图，三个质点a、b、c质量分别为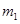
、
、
（
）。在c的万有引力作用下，a、b在同一平面内绕c沿逆时针方向做匀速圆周运动，轨道半径之比
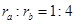,则它们的周期之比
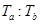=______;从图示位置开始，在b运动一周的过程中，a、b、c共线了____次。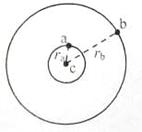 
我国航天计划的下一目标是登上月球，当飞船靠近月球表面的圆形轨道绕行几圈后登陆月球，飞船上备有以下实验器材：A计时表一只；B弹簧测力计一个；C已知质量为m的物体一个；D天平一只(附砝码一盒)．已知宇航员在绕行时及着陆后各做了一次测量，依据测量的数据，可求出月球的半径R及月球的质量M(已知引力常量为G)
(1)两次测量不需要选用的器材为________ (填选项前的字母)．
(2)两次测量的物理量是____ ____和_____ ___．
(3)试用所给物理量的符号分别写出月球半径R和质量M的表达式．
R＝______ __，M＝_____ ___.
地球绕太阳公转的周期为T1，轨道半径为R1，月球绕地球公转的周期为T2，轨道半径为R2，则地球绕太阳公转的线速度与月球绕地球公转的线速度之比为 ，太阳的质量是地球质量的 倍。
宇宙中存在由质量相等的四颗星组成的四星系统，四星系统离其他恒星较远，通常可忽略其他星体对四星系统的引力作用.已观测到稳定的四星系统存在这样一种形式：有三颗星位于边长为a的等边三角形的三个项点上，并沿外接于等边三角形的圆形轨道运行，而第四颗星刚好位于三角形的中心不动. 已知每颗星体质量均为m, 引力常量为G，星体运动的周期T=___________________。
在一个行星上，一昼夜的时间为T,若在行星上用弹簧秤测同一物体的重力，发现在赤道上仅为在两极的90%．设想该行星的自转角速度加快到某一值时，赤道上的物体会自动飘起来．则该行星上的一昼夜时间是________________
对于太阳的九大行星来说,轨道半径较大的,周期较大.冥王星绕太阳运动的轨道半径约为地球绕太阳运动轨道半径的 40倍,它绕太阳运动一周需要____ 年.（用根式表示）
有质量的物体周围存在着引力场。万有引力和库仑力有类似的规律，因此我们可以用定义静电场场强的方法来定义引力场的场强。由此可得，与质量为M的质点相距r处的引力场场强的表达式为EG= ( )（万有引力恒量用G表示）
设地球绕太阳做匀速圆周运动,半径为R,速率为v,则太阳的质量可用v1､R和引力常量G表示为________.太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速率约为地球公转速率的7倍,轨道半径约为地球公转轨道半径的2×109倍.为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量,则银河系中恒星数目约为________.
我国探月的“嫦娥工程”已启动，在不久的将来宇航员将登上月球。假如宇航员的质量为m，他在月球上测得摆长为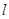
的单摆做小振幅振动的周期为T，将月球视为密度均匀、半径为r的球体，引力恒量为G，则宇航员在月球上的“重力”为________；月球的密度为________。
地球同步卫星到地心的距离可用地球质量
、地球自转周期
与引力常量
表示为
=。
银河系中有两颗行星绕某恒星运行，从天文望远镜中观察到它们的运转周期之比为27:1，则它们的轨道半径的比为___________________________。
某行星绕太阳运动可近似看作匀速圆周运动，已知行星运动的轨道半径为，周期为
，万有引力恒量为
，则该行星的线速度大小为；太阳的质量可表示为。
粤公网安备 44130202000953号