高中物理万有引力定律及其应用计算题

“嫦娥一号” 的成功发射，为实现中华民族几千年的奔月梦想迈出了重要的一步。已知“嫦娥一号”绕月飞行轨道可以近似看成圆周，距月球表面的高度为H，飞行周期为T,月球的半径为R，万有引力常量为G，假设宇航员在飞船上,飞船在月球表面附近竖直平面内俯冲， 在最低点附近作半径为r的圆周运动，宇航员质量是m，飞船经过最低点时的速度是v；。求：
(1)月球的质量M是多大？
(2)经过最低点时，座位对宇航员的作用力F是多大？

某同学是一位航天科技爱好者，当他从新闻中得知，中国航天科技集团公司将在2010年底为青少年发射第一颗科学实验卫星——“希望一号”卫星（代号XW-1）时，他立刻从网上搜索有关“希望一号”卫星的信息，其中一份资料中给出该卫星运行周期10.9min。他根据所学知识计算出绕地卫星的周期不可能小于83min，从而断定此数据有误。
已知地球的半径R=6.4×10⁶m，地球表面的重力加速度g=10m/s²。请你通过计算说明为什么发射一颗周期小于83min的绕地球运行的人造地球卫星是不可能的。

“嫦娥一号”的成功发射，为实现中华民族几千年的奔月梦想迈出了重要的一步.如图所示，“嫦娥一号”先进入绕月飞行的椭圆轨道，然后再椭圆轨道近月点变轨进入绕月飞行圆轨道；已知“嫦娥一号”绕月飞行的椭圆轨道远月点距月球表面高度为；又已知“嫦娥一号”绕月圆轨道飞行时，距月球表面的高度为，飞行周期为，月球的半径为，万有引力常量为；再后，假设宇航長在飞船上，操控飞船在月球表面附近竖直平面内俯冲，在最低点附近作半径为的圆周运动，宇航员质量是，飞船经过最低点时的速度是．求：

（1）月球的质量是多大？
（2）“嫦娥一号”经绕月飞行的椭圆轨道远月点时的加速度多大？“嫦娥一号”经绕月飞行的椭圆轨道近月点时欲变轨进入如图圆轨道，应该向前还是向后喷气？
（3）操控飞船在月球表面附近竖直平面内俯冲经过最低点时，座位对宇航员的作用力是多大？

航天员在月球表面完成了如下实验：如图所示，在月球表面固定一竖直光滑圆形轨道，在轨道内的最低点，放一可视为质点的小球，当给小球水平初速度v₀时，小球刚好能在竖直面内做完整的圆周运动。已知圆形轨道半径为r，月球的半径为R 。若在月球表面上发射一颗环月卫星，求最小发射速度。

(10分)天文观测到某行星有一颗以半径r、周期T环绕该行星做圆周运动的卫星，已知卫星质量为m．求：
（1）该行星的质量M是多大?
（2）如果该行星的半径是卫星运动轨道半径的1/10，那么行星表面处的重力加速度是多大?

宇航员在一星球表面上的某高处，沿水平方向抛出一个小球，经时间t，小球落到星球表面，测出抛出点与落地点之间距离为L。若抛出时的初速增大到原来的2倍，则抛出点到落地点间的距离为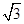L。已知两落地点在同一水平面上，该星球的质量M，万有引力常数为G，求:
（1）该星球的半径R。 
（2）该星球上的第一宇宙速度。

已知地球半径为R，地球表面处的重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v的表达式；
（2）若已知地球自转的周期为T，求地球同步卫星距离地面的高度h。

“嫦娥一号”探月卫星为绕月极地卫星.利用该卫星可对月球进行成像探测.设卫星在绕月极地轨道上做匀速圆周运动时距月球表面的高度为H，绕行周期为T_M；月球绕地球公转的周期为T_E，轨道半径为R₀；地球半径为R_E，月球半径为R_M.已知光速为c.

（1）如图所示，当绕月极地轨道的平面与月球绕地球公转的轨道平面垂直时（即与地心到月心的连线垂直时），求绕月极地卫星向地球地面发送照片需要的最短时间；
（2）忽略地球引力、太阳引力对绕月卫星的影响，求月球与地球的质量之比.

宇航员到了某星球后做了如下实验：如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角2θ。当圆锥和球一起以周期T匀速转动时，球恰好对锥面无压力．已知星球的半径为R，万有引力常量为G．求：

（1）线的拉力；
（2）该星球表面的重力加速度；
（3）该星球的第一宇宙速度；
（4）该星球的密度．

在物理学中，常常用等效替代、类比、微小量放大等方法来研究问题。如在牛顿发现万有引力定律一百多年后，卡文迪许利用微小量放大法由实验测出了万有引力常量G的数值，图所示是卡文迪许扭秤实验示意图。卡文迪许的实验常被称为是“称量地球质量”的实验，因为由G的数值及其他已知量，就可计算出地球的质量，卡文迪许也因此被誉为第一个称量地球的人。

（1）若在某次实验中，卡文迪许测出质量分别为m₁、m₂相距为r的两个小球之间引力的大小为F，求万有引力常量G；
（2）若已知地球半径为R，地球表面重力加速度为g，万有引力常量为G，忽略地球自转的影响，请推导出地球质量及地球平均密度的表达式。

我国“嫦娥一号”月球探测器在绕月球成功运行之后，为进一步探测月球的详细情况，又发射了一颗绕月球表面飞行的科学试验卫星，假设该卫星绕月球的运动视为圆周运动，并已知月球半径为R，月球表面重力加速度为g，万有引力常量为G，不考虑月球自转的影响．
(1)求该卫星环绕月球运行的第一宇宙速度v₁；
(2)若该卫星在没有到达月球表面之前先要在距月球某一高度绕月球做圆周运动进行调姿，且该卫星此时运行周期为T，求该卫星此时的运行半径r；
(3)由题目所给条件，请提出一种估算月球平均密度的方法，并推导出密度表达式．

两个行星各有一个卫星绕其表面运行，已知两个卫星的周期之比为1：3，两行星半径之比为3：1，则：
（1）两行星密度之比为多少？
（2）两行星表面处重力加速度之比为多少？

有一极地卫星绕地球做匀速圆周运动，该卫星的运动周期为T₀/4，其中T₀为地球的自转周期．已知地球表面的重力加速度为g，地球半径为R.．求：
（1）该卫星一昼夜经过赤道上空的次数n为多少？试说明理由。
（2）该卫星离地面的高度H．

土星上空有许多大小不等的岩石颗粒，其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为r_A＝8.0×10⁴ km和r _B＝1.2×10⁵ km。忽略所有岩石颗粒间的相互作用。（结果可用根式表示）
⑴求岩石颗粒A和B的线速度之比；
⑵求岩石颗粒A和B的周期之比；
⑶土星探测器上有一物体，在地球上重为10 N，推算出他在距土星中心3.2×10⁵ km处受到土星的引力为0.38 N。已知地球半径为6.4×10³ km，请估算土星质量是地球质量的多少倍？

太阳围绕银河系中心的运动可视为匀速圆周运动，其运动速度约为地球公转速度的7倍，轨道半径约为地球公转道半径的2×10⁹倍，为了粗略估算银河系中恒星的数目，可认为银河系中所有恒星的质量都集中在银河系中心，且银河系中恒星的平均质量约等于太阳质量，则银河系中恒星数目约为

A．10^9

B．10^11

C．10^13

D．10^15