宇航员到了某星球后做了如下实验：如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角2θ。当圆锥和球一起以周期T匀速转动时，球恰好对锥面无压力．已知星球的半径为R，万有引力常量为G．求：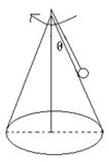
（1）线的拉力；
（2）该星球表面的重力加速度；
（3）该星球的第一宇宙速度；
（4）该星球的密度．
相关试题
（满分10分）如图所示，边长为L的正方形线框abcd的匝数为n，ad的中点和bc边的中点的连线OO′恰好位于匀强磁场的边界上，磁感应强度为B，线圈与外电阻R构成闭合电路，整个线圈的电阻也为R，现在让线圈以OO′为轴，以角速度ω匀速转动，求：
（1）若从图示位置开始计时，闭合电路中感应电动势的瞬时值表达式。
（2）线框从图示位置时转过90°的过程中电阻R上产生的热量和通过电阻R的电荷量
（满分7分）如图所示,实线为简谐波在t时刻的波形图,虚线为波在(t+0.01)s时刻的波形图,若波速为100m／s.
（1）指出简谐波的传播方向；
（2）x=1m处的质点在此0.01s内的位移多大?方向如何?
已知某星球赤道上有一物体质量为m，重力加速度为a，(不考虑星球自转带来的影响)，随星球自转的周期为T，星球半径为R，引力常量为G，求
（1）该星球的平均密度；
（2）该星球的第一宇宙速度；
（3）该星球的同步卫星离星球表面的高度。
如图所示，半径为R，管内径很小的光滑半圆管道竖直放置在距离地面为h的平台的边缘，质量为m的A、B两个小球先后以不同速度从底端进入管内，小球通过最高点C时，A对外管壁的压力大小为3mg， B对内管壁的压力大小为0.75mg.求A、B两小球落地点之间的水平距离.(都落在水平地面上)
相关知识点
粤公网安备 44130202000953号