高中物理万有引力定律及其应用计算题

航天员在月球上做自由落体实验，将某物体由距离月球表面高h处由静止释放，经时间t落到月球表面，已知月球半径为R，万有引力常量为G。试求：
（1）月球表面处重力加速度g的大小；
（2）月球的质量
（3）飞船在月球表面附近绕月球做匀速圆周运动的速度大小。

(12分)如图为宇宙中有一个恒星系的示意图，A为该星系的一颗星，它绕中央恒星O运动轨道近似为圆，天文学家观测得到A行星运动的轨道半径为R，周期为T   

(1)中央恒星O的质量是多大?
(2)长期观测发现，A行星实际运动的轨道与圆轨道总存在一些偏离，且周期性地每隔t时间发生一次最大的偏离，天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一平面内，且与A的绕行方向相同)，它对A行星的万有引力引起A轨道的偏离．根据上述现象及假设，预测未知行星B绕中央恒星O运行轨道半径有多大?

如图所示，宇航员站在某质量分布均匀的星球表面斜坡上，从P点沿水平方向以初速度v₀抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为α，已知该星球半径为R，万有引力常量为G，求：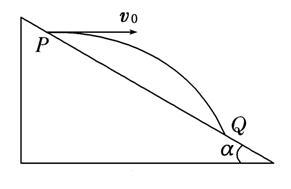

(1)该星球表面的重力加速度；
(2)该星球的第一宇宙速度v；
(3)该星球的密度。

一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小。已知地球半径R=6400km，地球表面重力加速度g=10m/s².

某恒星远处有一颗行星，靠近行星周围有众多的卫星，且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动，通过天文观测，测得离该行星最近的一颗卫星运动的轨道半径为，周期为。已知万有引力常量为G。
（1）求该行星的质量；
（2）通过天文观测，发现离该行星很远处还有一颗卫星，其运动的轨道半径为，周期为，试估算该行星周围众多卫星的总质量。
（3）通过天文观测发现，某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上，求再经过多长时间它们又将分布在一条直线上。

人们通过对月相的观测发现，当月球恰好是上弦月时，如图甲所示，人们的视线方向与太阳光照射月球的方向正好是垂直的，测出地球与太阳的连线和地球与月球的连线之间的夹角为θ.当月球正好是满月时，如图乙所示，太阳、地球、月球大致在一条直线上且地球在太阳和月球之间，这时人们看到的月球和在白天看到的太阳一样大(从物体两端引出的光线在人眼光心处所成的夹角叫做视角，物体在视网膜上所成像的大小决定于视角)．已知嫦娥飞船贴近月球表面做匀速圆周运动的周期为T，月球表面的重力加速度为g0，试估算太阳的半径．

已知月球的质量是地球质量的，月球半径是地球半径的，在月球表面16m处让质量m=50kg的物体自由下落，（已知地球表面的重力加速度g=10m/s²）。求：
（1）月球表面的重力加速度是多大？
（2）物体下落到月球表面所用的时间t是多少？
（3）月球的第一宇宙速度是地球的第一宇宙速度的多少倍？

航天宇航员在月球表面完成了如下实验：如图所示，在月球表面固定一竖直光滑圆形轨道，在轨道内的最低点，放一可视为质点的小球，当给小球水平初速度v₀时，小球刚好能在竖直面内做完整的圆周运动。已知圆形轨道半径为r，月球的半径为R。求：

（1）月球表面的重力加速度g；
（2）轨道半径为2R的环月卫星周期T。

物体在万有引力场中具有的势能叫做引力势能。取两物体相距无穷远时的引力势能为零，一个质量为的质点距离质量为M₀的引力源中心为时。其引力势能（式中G为引力常数）。现有一颗质量为的人造地球卫星以圆形轨道环绕地球飞行，由于受高空稀薄空气的阻力作用，卫星的圆轨道半径从缓慢减小到。已知地球的半径为R，地球表面的重力加速度为g，求此过程中卫星克服空气阻力做功。（用m、R、g、、表示）

分已知“嫦娥一号”绕月飞行轨道近似为圆形，距月球表面高度为H，飞行周期为T，
月球的半径为R，引力常量为G。求：
（1）“嫦娥一号”绕月飞行时的线速度大小；
（2）月球的质量；
（3）若发射一颗绕月球表面做匀速圆周运动的近月飞船，则其绕月运行的线速度应为多大．

2008年9月25日21时10分，神舟七号飞船成功发射，共飞行2天20小时27分钟，绕地球飞行45圈后，于9月28日17时37分安全着陆．航天员翟志刚着“飞天”舱外航天服，在刘伯明的配合下，成功完成了空间出舱活动，进行了太空行走．出舱活动结束后，释放了伴飞卫星，并围绕轨道舱进行伴飞试验．神舟七号是由长征—2F运载火箭将其送入近地点为A、远地点为B的椭圆轨道上，实施变轨后，进入预定圆轨道，其简化的模拟轨道如图所示．假设近地点A距地面高度为h，飞船在预定圆轨道上飞行n圈所用时间为t，地球表面的重力加速度为g，地球半径为R，试求：

（1）飞船在近地点A的加速度a_A大小；
（2）飞船在预定圆轨道上飞行速度v的大小．

(8分)荡秋千是大家喜爱的一项体育活动.随着科技的迅速发展,将来的某一天,同学们也许会在其他星球上享受荡秋千的乐趣.假设你当时所在星球的质量是M、半径为R,可将人视为质点,秋千质量不计、摆长不变、摆角小于90°,万有引力常量为G.那么,
（1）该星球表面附近的重力加速度g_星等于多少？
（2）若经过最低位置的速度为v₀,你能上升的最大高度是多少？

我国“神舟”六号宇宙飞船已经发射成功，当时在飞船控制中心的大屏幕上出现的一幅卫星运行轨迹图，如图所示，它记录了“神舟”六号飞船在地球表面垂直投影的位置变化。图中表示在一段时间内飞船绕地球圆周飞行四圈，依次飞经中国和太平洋地区的四次轨迹①、②、③、④，图中分别标出了各地点的经纬度（如：在轨迹①通过赤道时的经度为西经156°，绕行一圈后轨迹②再次经过赤道时经度为180°……），若已知地球半径为R，地球表面处的重力加速度g，地球自转周期为24h，根据图中的信息：

（1）如果飞船运行周期用T表示，试写出飞船离地面高度的表达式
（2）飞船运行一周，地球转过的角度是多少？
（3）求飞船运行的周期

宇航员在地球表面以一定初速度竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度竖直上抛同一小球，需经过时间5t小球落回原地．(取地球表面重力加速度g＝10 m/s²，阻力不计)
(1)求该星球表面附近的重力加速度g′；
(2)已知该星球的半径与地球半径之比为R_星∶R_地＝1∶4，求该星球的质量与地球质量之比M_星∶M_地．

(14分) 神舟五号载人飞船在绕地球飞行的第5圈进行变轨，由原来的椭圆轨道变为距地面高度h的圆形轨道，已知地球半径R，地面处的重力加速度为g．求飞船在上述圆轨道上运行的周期T．