在某星球上,宇航员做了一个实验:让质量为m="1." 0 kg的小滑块以v0="6" m/s的初速度从倾角为θ= 530的斜面AB的顶点A滑下,到达B点后与垂直斜面的挡板碰撞,不计碰撞时的机械能损失.滑块与斜面间的动摩擦因数为 =" 0." 5,测得A点离B点所在水平面的高度为h=3m,最终物块在斜面上通过的路程s =" 20" m.已知sin 530 =" 0." 8 ,cos 530="0." 6,不计该星球的自转以及其他星球对它的作用.
=" 0." 5,测得A点离B点所在水平面的高度为h=3m,最终物块在斜面上通过的路程s =" 20" m.已知sin 530 =" 0." 8 ,cos 530="0." 6,不计该星球的自转以及其他星球对它的作用.
(1)求该星球表面的重力加速度g;
(2)若测得该星球的半径为R=6 106 m,则该星球的第一宇宙速度为多大?
106 m,则该星球的第一宇宙速度为多大?
(3)取地球半径Ro=6.4 106m,地球表面的重力加速度g0=10 m/s2,求该星球的平均密度与地球的平均密度之比
106m,地球表面的重力加速度g0=10 m/s2,求该星球的平均密度与地球的平均密度之比 .
.
2008年我国成功实施了“神舟七号”载人飞船航天飞行,“神舟七号”飞行到31圈时,成功释放了伴飞小卫星,通过伴飞小卫星可以拍摄“神舟七号”的运行情况.若在无牵连的情况下伴飞小卫星与“神舟七号”保持相对静止.下述说法中正确的是( )
| A.伴飞小卫星和“神舟七号”飞船有相同的角速度 |
| B.伴飞小卫星绕地球沿圆轨道运动的速度比第一宇宙速度大 |
| C.宇航员在太空中的加速度小于地面上的重力加速度 |
| D.宇航员在太空中不受地球的万有引力作用,处于完全失重状态 |
据天文学观测,某行星在距离其表面高度等于该行星半径3倍处有一颗同步卫星。已知该行星的平均密度与地球的平均密度相等,地球表面附近绕地球做匀速圆周运动的卫星周期为T,则该行星的自转周期为( )
| A.3 T | B.4T | C. T T |
D.8T |
欧洲天文学家发现了可能适合人类居住的行星“格里斯581c”.该行星的质量是地球的 倍,直径是地球的
倍,直径是地球的 倍.设在该行星表面及地球表面发射人造卫星的最小发射速度分别为
倍.设在该行星表面及地球表面发射人造卫星的最小发射速度分别为 ,则
,则 的比值为( )
的比值为( )
A. |
B. |
C. |
D. |
某星球半径为R =" 6×" 106 m,假设该星球表面上有一倾角为θ = 30°的固定斜面,一质量为m =" 1" kg的小物块在力,作用下从静止开始沿斜面向上运动,力F始终与斜面平行,如图甲所示。已知小物块和斜面间的动摩擦因数 ,力F随位移x变化的规律如图乙所示(取沿斜面向上的方向为正向),如果小物块运动12 m时速度恰好为零,已知万有引力常量G =" 6.67" × 10-11 N·m2/kg2。试求:(计算结果保留一位有效数字)
,力F随位移x变化的规律如图乙所示(取沿斜面向上的方向为正向),如果小物块运动12 m时速度恰好为零,已知万有引力常量G =" 6.67" × 10-11 N·m2/kg2。试求:(计算结果保留一位有效数字)
(1)该星球表面上的重力加速度g的大小;
(2)该星球的平均密度。
英国《每日邮报》网站2015年4月3日发表了题为《NASA有能力在2033年将宇航员送入火星轨道并在2039年首次登陆火星》的报道,如图是人类登陆火星想象图。已知火星半径是地球半径的 ,质量是地球质量的
,质量是地球质量的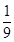 ,自转周期基本相同。地球表面重力加速度是g,若宇航员在地面上能向上跳起的最大高度是h,在忽略自转影响的条件下,下述分析正确的是:
,自转周期基本相同。地球表面重力加速度是g,若宇航员在地面上能向上跳起的最大高度是h,在忽略自转影响的条件下,下述分析正确的是:
A.火星表面的重力加速度是 |
B.宇航员在火星上向上跳起的最大高度是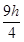 |
C.火星的第一宇宙速度是地球第一宇宙速度的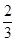 倍 倍 |
D.宇航员在火星表面所受火星引力是他在地球表面所受地球引力的 倍 倍 |
已知月球半径为R,飞船在距月球表面高度为R的圆轨道上飞行,周期为T,万有引力常量为G,下列说法正确的是
A.月球第一宇宙速度为 |
B.月球表面重力加速度为 |
C.月球密度为 |
D.月球质量为 |
设地球自转周期为T,质量为M,引力常量为G,假设地球可视为质量均匀分布的球体,半径为R。同一物体在南极和赤道水平面上静止时所受到的支持力之比为( )
A.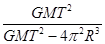 |
B. |
C.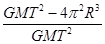 |
D. |
宇航员在月球表面完成下面实验:在一固定的竖直光滑圆弧轨道内部的最低点,静止一质量为m的小球(可视为质点),如图所示,当给小球水平初速度υ0时,刚好能使小球在竖直平面内做完整的圆周运动。已知圆弧轨道半径为r,月球的半径为R,万有引力常量为G。若在月球表面上发射一颗环月卫星,所需最小发射速度为( )

A. |
B. |
C. |
D. |
太阳系各行星几乎在同一平面内沿同一方向绕太阳做圆周运动,当地球恰好运行到某个行星和太阳之间,且三者几乎成一条直线的现象,天文学成为“行星冲日”据报道,2014年各行星冲日时间分别是:1月6日,木星冲日,4月9日火星冲日,6月11日土星冲日,8月29日,海王星冲日,10月8日,天王星冲日,已知地球轨道以外的行星绕太阳运动的轨道半径如下表所示,则下列判断正确的是:( )
| |
地球 |
火星 |
木星 |
土星 |
天王星 |
海王星 |
| 轨道半径(AU) |
1.0 |
1.5 |
5.2 |
9.5 |
19 |
30 |
A各点外行星每年都会出现冲日现象
B.在2015年内一定会出现木星冲日
C.天王星相邻两次的冲日的时间是土星的一半
D.地外行星中海王星相邻两次冲日间隔时间最短
如图,甲、乙两颗卫星以相同的轨道半径分别绕质量为M和2M的行星做匀速圆周运动,下列说法正确的是
| A.甲的向心加速度比乙的小 |
| B.甲的运行周期比乙的小 |
| C.甲的线速度比乙的小 |
| D.甲的角速度比乙的大 |
如图所示为我国“嫦娥一号卫星”从发射到进入月球工作轨道的过程示意图。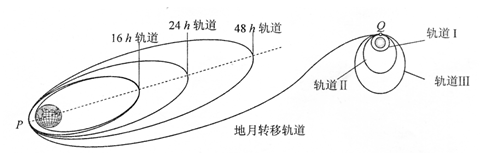
在发射过程中经过一系列的加速和变轨,卫星沿绕地球“48小时轨道”在抵达近地点P时,主发动机启动,“嫦娥一号卫星”的速度在很短时间内由v1提高到v2,进入“地月转移轨道”,开始了从地球向月球的飞越。“嫦娥一号卫星”在“地月转移轨道”上经过114小时飞行到达近月点Q时,需要及时制动,使其成为月球卫星。之后,又在绕月球轨道上的近月点Q经过两次制动,最终进入绕月球的圆形工作轨道I。已知“嫦娥一号卫星”质量为m0,在绕月球的圆形工作轨道I上运动的周期为T,月球的半径r月,月球的质量为m月,万有引力恒量为G。
(1)求卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功(不计地球引力做功和卫星质量变化);
(2)求“嫦娥一号卫星”在绕月球圆形工作轨道I运动时距月球表面的高度;
(3)理论表明:质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为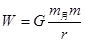 。为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道I的高度,最终进入圆形工作轨道,其第一次制动后的速度大小理论上应满足什么条件?
。为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道I的高度,最终进入圆形工作轨道,其第一次制动后的速度大小理论上应满足什么条件?
(由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同:若地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为T,引力常量为G,地球可视为质量均匀分布的球体。求: (1)地球半径R;(2)地球的平均密度;
(3)若地球自转速度加快,当赤道上的物体恰好能“飘”起来时,求地球自转周期T'。
一个质量为1500 kg行星探测器从某行星表面竖直升空,发射时发动机推力恒定,发射升空后8 s末,发动机突然间发生故障而关闭;如图所示为探测器从发射到落回出发点全过程的速度图象;已知该行星表面没有大气,不考虑探测器总质量的变化;求: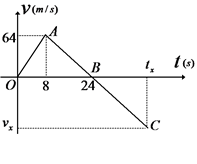
(1)探测器在行星表面上升达到的最大高度;
(2)探测器落回出发点时的速度;
(3)探测器发动机正常工作时的推力。