如图所示,甲、乙两快艇在湖面上做匀速圆周运动。关于两快艇的运动,下列说法正确的是()
| A.若两快艇运动的周期相等,半径较小的向心加速度较大 |
| B.若两快艇运动的线速度大小相等,半径较小的向心加速度较大 |
| C.若两快艇运动的角速度相等,半径较小的向心加速度较大 |
| D.若两快艇运动的线速度大小相等,半径较大的向心加速度较大 |
如图所示,汽车过拱形桥时的运动可以看做匀速圆周运动,质量为m的汽车以速度v过桥,桥面的圆弧半径为R,重力加速度为g,则汽车通过桥面最高点时对桥面的压力大小为()
| A.mg | B. |
C.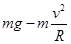 |
D. |
如图所示,BC是半径为R的竖直面内的圆弧轨道,轨道末端C在网心O的正下方,∠BOC= 60°,将质量为m的小球,从与O等高的A点水平抛出,小球恰好从B点沿圆弧切线方向进入网轨道,由于小球与圆弧之间有摩擦,能够使小球从B到C做匀速圆周运动。重力加速度大小为g.则
A.从B到C,小球克服摩擦力做功为
B.从B到C,小球与轨道之间的动摩擦因数可能保持不变
C. A、B两点间的距离为
D.在C点,小球对轨道的压力为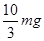
2013年6月20日,航天员王亚平在“天宫一号”舱内授课,演示了小球做匀速圆周运动。小球运动过程中一定会发生变化的是
| A.速度大小 | B.速度方向 | C.加速度大小 | D.角速度大小 |
计算机硬盘内部结构如图所示,读写磁头在计算机的指令下移动到某个位置,硬盘盘面在电机的带动下高速旋转,通过读写磁头读写下方磁盘上的数据.磁盘上分为若干个同心环状的磁道,每个磁道按圆心角等分为18个扇区.现在普通的家用电脑中的硬盘的转速通常有5400r/min和7200r/min两种,硬盘盘面的大小相同,则()
| A.磁头的位置相同时,7200r/min的硬盘读写数据更快 |
| B.对于某种硬盘,磁头离盘面中心距离越远,磁头经过一个扇区所用的时间越长 |
| C.不管磁头位于何处,5400r/min的硬盘磁头经过一个扇区所用时间都相等 |
| D.5400r/min与7200r/min的硬盘盘面边缘的某点的向心加速度的大小之比为3:4 |
如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l。木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是: ()
| A.b一定比a先开始滑动 |
| B.a、b所受的摩擦力始终相等 |
C.ω= 是b开始滑动的临界角速度 是b开始滑动的临界角速度 |
D.当ω= 时,a所受摩擦力的大小为kmg 时,a所受摩擦力的大小为kmg |
如图所示,一带负电的金属圆环绕轴OO '以角速度ω匀速旋转,在环左侧轴线上的可以自由转动小磁针最后静止时N极的位置是()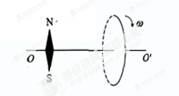
| A.竖直向上 | B.竖直向下 |
| C.沿轴线向左 | D.沿轴线向右 |
如图是质谱仪工作原理的示意图.带电粒子a、b经电压U加速(在A点初速度为零)后,进入磁感应强度为B的匀强磁场做匀速圆周运动,最后分别打在感光板S上的x1、x2处.图中半圆形的虚线分别表示带电粒子a、b所通过的路径,则()
| A.a的质量一定大于b的质量 |
| B.a的电荷量一定大于b的电荷量 |
| C.a运动的时间小于b运动的时间 |
D.a的比荷( )小于b的比荷( )小于b的比荷( ) ) |
物体做匀速圆周运动,下列说法正确的是()
| A.它所受的合外力一定是变力 |
| B.它所受的合外力一定是恒力 |
| C.它所受的合外力方向不一定指向圆心 |
| D.它处于平衡状态,它所受的合外力为零 |
如图所示,一个质量为m的小球绕圆心O做匀速圆周运动.已知圆的半径为r,小球运动的角速度为ω,则它所受向心力的大小为()
A.m |
B.mωr | C.mωr2 | D.mω2r |
如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动。忽略重力的影响,求:
(1)匀强电场的电场强度E的大小。
(2)粒子从电场射出时速度v的大小。
(3)粒子在磁场中做匀速圆周运动的半径R。
如图所示,匀速转动的水平圆盘上放有质量分别为2kg和3kg的小物体A、B,A、B间用细线沿半径方向相连。它们到转轴的距离分别为RA=0.2m、RB=0.3m。A、B与盘面间的最大静摩擦力均为重力的0.4倍。g取10m/s2,现极其缓慢地增大圆盘的角速度,则下列说法正确的是()
A.小物体A达到最大静摩擦力时,B受到的摩擦力大小为12N
B.当A恰好达到最大静摩擦力时,圆盘的角速度为4rad/s
C.细线上开始有弹力时,圆盘的角速度为
D.某时刻剪断细线,A将做向心运动,B将做离心运动
质量为m的小球由轻绳a和b分别系于一轻质细杆的A点和B点,如图所示,绳a与水平方向成θ角,绳b沿水平方向且长为l,当轻杆绕轴AB以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,则下列说法正确的是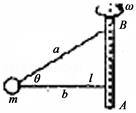
| A.a绳张力不可能为零 |
| B.a绳的张力随角速度的增大而增大 |
C.当角速度 ,b绳将出现弹力 ,b绳将出现弹力 |
| D.若b绳突然被剪断,a绳的弹力可能不变 |
如图所示,轻杆的一端用铰链固定在竖直转轴OO′上的O端,另一端固定一小球,轻杆可在竖直平面内自由转动,当转轴以某一角速度匀速转动时,小球在水平面内做匀速圆周转动,此时轻杆与竖直转轴OO′的夹角为37°.已知转轴O端距离水平地面的高度为h,轻杆长度为L,小球的质量为m,重力加速度为g,取sin37°≈0.6,cos37°≈0.8,求:
(1)小球做匀速圆周运动的线速度v.
(2)若某时刻小球从轻杆上脱落,小球的落地点到转轴的水平距离d.
(3)若缓慢增大转轴的转速,求轻杆与转轴的夹角从37°增加到53°的过程中,轻杆对小球所做的功W.