如图所示皮带转动轮，大轮直径是小轮直径的2 倍，A是大轮边缘上一点，B是小轮边缘上一点， C是大轮上一点，C到圆心O1的距离等于小轮半径。 转动时皮带不打滑，则A、B两点的角速度之比ωA：ωB＝_ ，B、C两点向心加速度大小之比
：
＝ 。
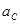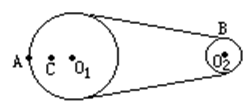
质量为m的小球由轻绳a和b系于一轻质木架上的A点和C点，且La＜Lb , 如图所示。当轻杆绕轴BC以角速度ω匀速转动时，小球在水平面内作匀速圆周运动，绳a在竖直方向、绳b在水平方向。当小球运动在图示位置时，绳b被烧断的同时杆也停止转动，则 ( )
| A．小球仍在水平面内作匀速圆周运动 |
| B．在绳被烧断瞬间，a绳中张力突然增大 |
| C．在绳被烧断瞬间，小球所受的合外力突然变小 |
| D．若角速度ω较大，小球可以在垂直于平面ABC的竖直平面内作圆周运动 |
在绕地球作匀速圆周运动的太空仓内，按照同学们使用的新人教版教材要求，能完成的实验是：
| A．验证力的平行四边形法则 |
| B．探究弹簧形变量与弹力的关系 |
| C．探究物体加速度与质量和合外力的关系 |
| D．用平抛运动测初速度 |
甲、乙两物体都做匀速圆周运动，其质量之比为1：2，转动半径之比为1：2，在相等时间里甲转过30°，乙转过45°，则它们所受外力的合力之比为 （ ）
| A．1：4 | B．1：6 | C．9：16 | D．1：9 |
如图所示，三段细线长OA=AB=BC， A、B、C三球质量相等，当它们绕O点在光滑的水平桌面上以相同的角速度作匀速圆周运动时，则三段线的拉力TOA:TAB:TBC为（ ）
A．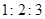
B．
C．
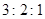D．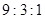
“飞车走壁”杂技表演简化后的模型如图所示，表演者沿表演台的侧壁做匀速圆周运动。若表演时杂技演员和摩托车的总质量不变，摩托车与侧壁间沿侧壁倾斜方向的摩擦力恰好为零，轨道平面离地面的高度为H，侧壁倾斜角度α不变，则下列说法中正确的是（ ） 
| A．摩托车做圆周运动的H越高，角速度越小 |
| B．摩托车做圆周运动的H越高，线速度越小 |
| C．摩托车做圆周运动的H越高，向心力越大 |
| D．摩托车对侧壁的压力随高度H变大而减小 |
一半径为R的雨伞绕柄以角速度
匀速旋转，如右图所示，伞边缘距地面高h，甩出的水滴在地面上形成一个半径为r的圆，则角速度的表达式为( )
A． |
B． |
C． |
D． |
如图所示，A.B两个小球，质量相等，用一根轻绳相连，另有一根轻绳的两端分别连接O点和B球，让两小球绕O点在光滑水平桌面上以相同的角速度做匀速圆周运动，若OB绳上的拉力为F1，AB绳上的拉力为F2，OB=2AB，则 ( )
A．F1：F2=2：3 B．F1：F2=3：2 C．F1：F2=5：3 D．F1：F2=2：1
如图所示，长为R的轻质杆（质量不计），一端系一质量为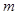
的小球（球大小不计），绕杆的另一端O在竖直平面内做匀速圆周运动，若小球最低点时，杆对球的拉力大小为1.5
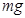，求：
①小球最低点时的线速度大小？
②小球通过最高点时，杆对球的作用力的大小及方向？
③小球以多大的线速度运动，通过最高处时杆对球不施力？
用长短不同、材料相同的同样粗细的绳子各拴着一个质量相同的小球在光滑水平面上做匀速圆周运动，如图所示，则( )
| A．两个小球以相同的线速度运动时，长绳易断 |
| B．两个小球以相同的角速度运动时，短绳易断 |
| C．两个小球以相同的角速度运动时，长绳易断 |
| D．以上说法都不对 |
下列说法错误的是 （ ）
| A．曲线运动一定有加速度 |
| B．平抛运动是一种匀变速曲线运动 |
| C．物体受到的合外力是恒力时不会做曲线运动 |
| D．匀速圆周运动是一种变加速曲线运动 |
汽车甲和汽车乙质量相等，以相等的速率沿同一水平弯道做匀速圆周运动，甲车在乙车的外侧。两车沿半径方向受到的摩擦力分别为f甲和f乙。以下说法正确的是
| A．f甲小于f乙 |
| B．f甲等于f乙 |
| C．f甲大于f乙 |
| D．f甲和f乙大小均与汽车速率无关 |
如图所示，一根细线下端拴一个金属小球
，细线的上端固定在金属块
上，放在带小孔（小孔光滑）的水平桌面上，小球在某一水平面内做匀速圆周运动（圆锥摆）。现使小球改到一个更高一些的水平面上做匀速圆周运动（图中
位置），两次金属块都静止在桌面上的同一点，则后一种情况与原来相比较，下面的判断中正确的是（ ）
| A．细线所受的拉力变小 |
B．小球 运动的角速度变小 |
| C．受到桌面的静摩擦力变大 |
| D．受到桌面的支持力变大 |
粤公网安备 44130202000953号
