高中物理匀速圆周运动试题

两个小球固定在一根长为L的杆的两端，绕杆上的固定点O做匀速圆周运动，如图，当小球1 的速度为v₁时，小球2 的速度为v₂，则转轴到球1的距离是         

宇宙飞船正在离地面高的轨道上做匀速圆周运动，飞船内一弹簧秤下悬挂一质量为m的重物，g为地面处重力加速度，则弹簧秤的读数为

A．mg

B．mg

C．mg

D．0

如图所示，在水平转台上放一个质量M=2kg的木块，它与转台间最大静摩擦力f_m=6.0N，绳的一端系住木块，穿过转台的中心孔O(孔光滑)，另一端悬挂一个质量m=1.0kg的物块，当转台以ω=5rad／s匀速转动时，木块相对转台静止，则木块M到O点的距离可能是(g=10m/s²，M、m均视为质点)：

A．0.04m

B．0.08m

C．0.16m

D．0.32m

如图所示，在匀速转动的水平圆盘上，沿半径方向放置两个用细线相连的质量均为m的小物体A、B，它们到转轴的距离分别为r_A="20" cm，r_B="30" cm，A、B与盘面间最大静摩擦力均为重力的0.4倍，试求：
（1）当细线上开始出现张力时，圆盘的角速度；
（2）当A开始滑动时，圆盘的角速度；
（3）当A即将滑动时，烧断细线，A、B运动状态如何？(g取10 m/s²)

如图所示，半径为R的球壳，内壁光滑，当球壳绕竖直方向的中心轴转动时，一个小物体恰好相对静止在球壳内的P点，OP连线与竖直轴夹角为θ．试问：球壳转动的周期多大？

如图，小球原来能在光滑的水平面上做匀速圆周运动，若剪断B、C之间的细绳，当A球重新达到稳定状态后，则A球的：（　　）
　　A、运动半径变大
　　B、速率变大
　　C、角速度变大
　　D、周期变大

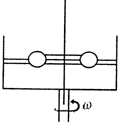
如图，在光滑的横杆穿着两质量分别为m₁、m₂的小球，小球用细线连接起来，当转台匀速转动时，下列说法正确的是：（　　）

A．两小球速率必相等

B．两小球角速度必相等

C．两小球加速度必相等

D．两小球到转轴距离与其质量成反比

如图所示为一皮带传动装置，右轮半径为r，a点在它的边缘上．左轮半径为2r，b点在它的边缘上。若在传动过程中，皮带不打滑，则a点与b点的向心加速度大小之比为（   ）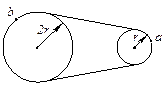

A．1：2

B．2：1

C．4：1

D．1：4

关于匀速圆周运动的向心力，以下说法正确的是（   ）

A．向心力是除物体所受重力、弹力及摩擦力以外的一种新力

B．向心力是做匀速圆周运动的物体所受的合力

C．向心力是线速度变化的原因

D．向心力是产生向心加速度的原因

关于质点的匀速圆周运动，下列说法正确的是（   ）

A．由a=可知，a与r成反比

B．由a=ω^2r可知，a与r成正比

C．由v=ωr可知，v与r成正比

D．由ω=2πn可知，ω与n成正比

在匀速圆周运动中，下列物理量不变的是（   ）

A．角速度	B．线速度
C．向心加速度	D．周期

下列关于匀速圆周运动的说法，正确的是（   ）

A．匀速圆周运动是匀速运动

B．匀速圆周运动是匀变速运动

C．匀速圆周运动是加速度不变的运动

D．匀速圆周运动是加速度不断改变的运动

如图5-4-8所示，在轮B上固定有同轴小轮A，轮B通过皮带带动轮C，皮带和两轮之间没有滑动，A、B、C三轮的半径依次为r₁、r₂、r₃.绕在A轮上的绳子，一端固定在A轮边缘上，另一端系有重物，当重物P以速度v匀速下降时，C轮转动的角速度为_____________.

图5-4-8

如图5-4-9所示是生产流水线上的皮带传输装置，传输带上等间距地放着很多半成品产品.A轮处装有光电计数器，它可以记录通过A处的产品数目，已经测得轮A、B的半径分别为r_A="20" cm、r_B="10" cm，相邻两产品距离为30 cm，1分钟内有41个产品通过A处（即从第一个产品到A处开始计时直至第四十一个产品到A处），求：

图5-4-9
（1）产品随传送带移动的速度大小；
（2）A、B轮轮缘上的两点P、Q及A轮半径中点M的线速度和角速度大小；
（3）如果A轮是通过摩擦带动C轮转动，且r_c="5" cm，求出C轮的角速度（轮不打滑）.

在水平转台上有一两端固定的水平横杆，杆上套一质量为m的小球（可视作质点）。球可沿杆无摩擦地滑动，现用两根劲度系数均为K的轻弹簧（也套在横杆上）将小球拴住，横杆与轴O在同一竖直平面内，轴O位于水平转台的中央，转台静止时两根弹簧均未有形变，小球所在点P轴O的距离为L，如图所示，转台以角速度ω绕竖直轴O旋转时，小球移到了另一点P′，与横杆保持相对静止，这时P′与P点之间的距离△L＝？